Scan0039

© J. Pelc WMT/77

WSTĘP DO METODY ELEMENTÓW SKOŃCZONYCH. PODSTAWOWE POJĘCIA.

Metoda Elementów Skończonych (MES) jest metodą:

•    numeryczną - działania na liczbach

•    dyskretną - operuje skończonym zbiorem wartości funkcji (wektory, macierze)

•    przybliżoną - na ogół otrzymujemy rozwiązania przybliżone, obarczone pewnym błędem w odniesieniu do rozwiązań ścisłych (analitycznych)

•    ogólną - stosowaną do rozwiązywania zadań wytrzymałości materiałów, przepływów ciepła, zagadnień elektromagnetycznych, mechaniki płynów itp.

•    skuteczną - pozwala rozwiązywać zadania, których nie daje się rozwiązać metodami analitycznymi (klasycznymi)

Pojęcia wstępne

Element skończony - myślowo wydzielona, mała część konstrukcji (pręt kratownicy, ramy, element tarczy, powłoki itp.)

© J. Pelc

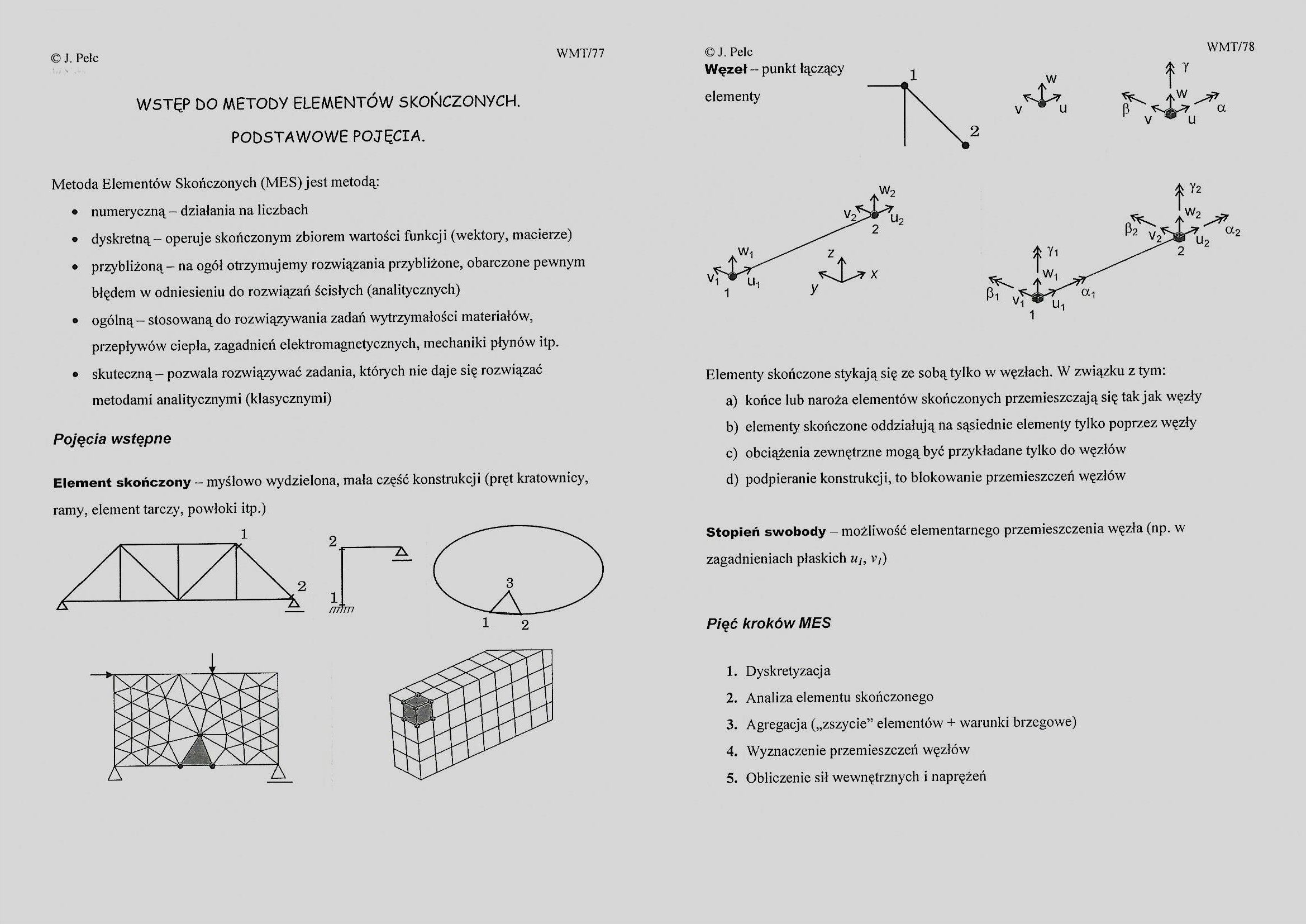
Węzeł -- punkt łączący elementy

Elementy skończone stykają się ze sobą tylko w węzłach. W związku z tym:

a)    końce lub naroża elementów skończonych przemieszczają się tak jak węzły

b)    elementy skończone oddziałują na sąsiednie elementy tylko poprzez węzły

c)    obciążenia zewnętrzne mogą być przykładane tylko do węzłów

d)    podpieranie konstrukcji, to blokowanie przemieszczeń węzłów

Stopień swobody - możliwość elementarnego przemieszczenia węzła (np. w zagadnieniach płaskich Uj, V/)

Pięć kroków MES

1.    Dyskretyzacja

2.    Analiza elementu skończonego

3.    Agregacja („zszycie” elementów + warunki brzegowe)

4.    Wyznaczenie przemieszczeń węzłów

5.    Obliczenie sił wewnętrznych i naprężeń