Scan0040

© J. Pelc WMT/79

Macierz sztywności elementu

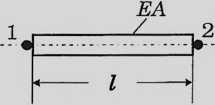
¹*-A/VW-»²

k

Al = —    Al = -

EA    k

k-~

I

W wyniku przemieszczeń węzłów elementu W/, u₂ pojawiają się siły sprężystości (tzn. pochodzące od sprężyny) działające na węzły. Siły sprężystości Sj i S₂ można wyrazić za pomocą przemieszczeń węzłów u/ i u₂:

5] = k(u_x - u₂ ) S₂ = k(u₂ - w,)

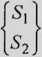
k -k J W] 1 -k k | u₂\

S = ku

k = k

1

-1

- nazywamy macierzą sztywności elementu

Należy zwrócić uwagę, że siły sprężystości działają na węzły przeciwnie do założonych dodatnich zwrotów przemieszczeń Uj i u₂.

-u₂)

Macierz sztywności układu (konstrukcji)

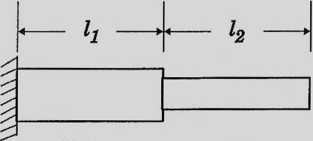
EjAi    ^2^2

Lifi

r^WWtAAAM

i

Wyznaczymy siły (wewnętrzne) działające na węzły rozważając kolejno przesunięcie tylko jednego z węzłów w danej chwili. Jeżeli przemieszczać się będą wszystkie węzły równocześnie, to towarzyszące temu stanowi siły obliczymy korzystając z zasady superpozycji (sumowanie poszczególnych składników).

Oznaczenie sił działających na węzły jest następujące:    Sij

gdzie / -nr węzła na który działa siła,/ - nr przemieszczanego węzła.

li J    li₂

rA/WWAAA/Vi

Sn = k_} U]

1)    Uj >0:    ć>2j — k^u^

®

$31 ~ 0

$12 ⁼ ~^l^u2

s, = IX

2)    U2 ^ 0: S₂2 — k^u₂ *i" k₂ił₂

M

S₃₂ = —k₂u₂

S13 ⁼ 0

3) u₃ > 0: *S₂3 ⁼ ~^2^U3 S33 ⁼ k₂u 2,

= k_lu_[ - k(U₂

5₂    - -k_lu_l + k_{u₂ + k₂u₂ - k₂u₃

5₃    — k₂tt₂ "i^- k₂u₃