Scan0026 2

HIPOTEZY WYTRZYMAŁOŚCIOWE

W projektowaniu konstrukcji inżynierskich, istotne zagadnienie stanowi ocena niebezpieczeństwa zniszczenia jej materiału.

Definicja 1: Jako miarę niebezpieczeństwa zniszczenia materiału konstrukcji przyjmuje się wartość funkcji wytężenia materiału W:

W-W(a„<7₂,<7₃)

Definicja 2: Hipoteza wytrzymałościowa jest pewnym twierdzeniem (założeniem) określającym postać funkcji wytężenia materiału W.

Mając tedy postać W można ocenić niebezpieczeństwo zniszczenia materiału, znajdującego się w złożonym (trójosiowym) stanie naprężenia, przez porównanie wartości funkcji jego wytężenia z wartością funkcji wytężenia materiału pręta rozciąganego osiowo:

W(a_ua₂, <7₃)= W((jj) -> a, = a = a_MSt = /(cr„ ct₂, <t₃)

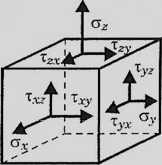
trójosiowy stan naprężenia <--> jednoosiowy stan naprężenia Pojęcie naprężenia zastępczego ą₂asi, zwanego też naprężeniem zredukowanym,

umożliwia ocenę wytężenia materiału za pomocą jednej liczby. Stąd warunek wytrzymałości, uwzględniający hipotezę wytrzymałościową, ma anaiogicznąjak dotychczas postać

Przy czym należy w materiale konstrukcji znaleźć wartość maksymalną tego naprężenia, tj. w powyższym warunku należy zawsze podstawiać a_zast = cr^^x = max[o\_av,(x, y, z)].

A-odpowiednie naprężenie dopuszczalne [MPa].

HIPOTEZA COULOMBA-TRESKI

Hipoteza ta, zwana również hipoteza największego naprężenia stycznego, głosi, że o zniszczeniu materiału decyduje wartość naprężenia stycznego. Jeżeli osiągnie ono wartość r_n, zwaną naprężeniem stycznym niszczącym, to nastąpi zniszczenie materiału.

tl

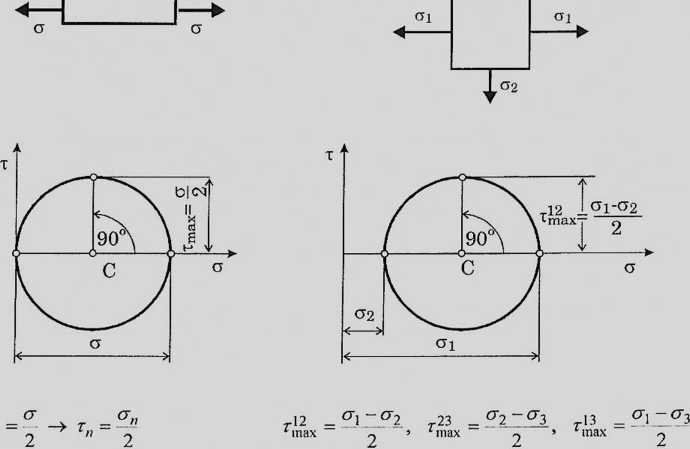
Zakłada się, że <j_)]r - cr_nc = a_tl.

Zgodnie z tą hipoteza materiał nie ulegnie zniszczeniu, jeżeli spełnione są warunki:

— T < T < T ¹ ti — *max ~~ /;

czyli, gdy każde z naprężeń r,'_n²ax, r ² _ax, r,^³ax spełnia powyższy warunek.

- cr„ < cT| -cr₂ - <- ograniczony obszar w przestrzeni (07, oy crj), określający

-a„<a₂-CT₃<<T„

-rr <rr -n- < rr bezpieczne dla danego materiału kombinacje naprężeń aj, 02, 03

(J_n — O | u₃ — <J_n