skanuj0068 (Kopiowanie)

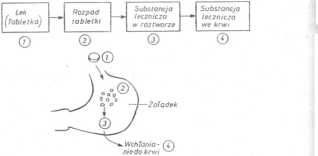
Ryc. 9.1. Schemat procesów poprzedzających pojawienie się substancji leczniczej w osoczu po doustnym podaniu leku w postaci tabletki

podania doustnego ten ostatni proces może mieć miejsce dopiero po uprzednim rozpadzie podanej postaci leku (tabletka, kapsułka) i uwolnieniu substancji leczniczej. Ilustruje to schemat przedstawiony na ryc. 9.1. i Uwzględnienie procesów wchłaniania substancji leczniczej i jej eliminacji, przebiegających wg schematu iak na ryc. 9.2., a więc przy założeniu; że dystrybucja przebiega szybciej od eliminacji i wchłaniania, pozwala

Substancja lecznicza w organizmie -

Lek w miejscu podania

Ryc. 9.2. Otwarty model jednokompartmcntowy dla podania pozanaczyniowego

przedstawić szybkość zmian ilości substancji leczniczej równaniem om( wionym na str. 25:

Szybkość zmian ilości substancji leczniczej w organizmie

Szybkość _ Szybkość

wchłaniania    eliminacji

Ze względu na to, że proces wchłaniania substancji leczniczej z miejsc jego podania jest w większości przypadków procesem I rzędu, wyrażeni to można zapisać:

(9.1

dA/dt - KFD-KA

w którym:

dA/dt — szybkość zmian ilości substancji leczniczej w organizmie, k_a — stała szybkości dla procesu wchłaniania,

134 Zarys biofarmacji

K — stała szybkości dla procesu eliminacji,

•d — ilość substancji leczniczej w organizmie,

F — ułamek dawki leku,

D — podana dawka leku.

Rozwiązanie równania 9.1 daje wyrażenie:

( A - FD)    (9-2)

Ponieważ zależność między ilością substancji leczniczej w organizmie, a jej stężeniem w osoczu określa równanie 8.6:

A = VtC

wobec tego dzieląc równanie 9.2 obustronnie przez V_d otrzymuje się wyrażenie:

<«>

opisujące przedstawiony na ryc. 9.3 przebieg zmian stężenia substancji leczniczej w osoczu obserwowany po jednorazowym podaniu pozanaczyniowym dawki D.

Ryc. 9.3. Przebieg zmian stężenia substancji leczniczej w osoczu po jednorazowym pozanaczyniowym podaniu leku

Z wykresu tego można zauważyć, że w wyniku pozanaczyniowego podania leku w dawce D stężenie substancji leczniczej zwiększa się od zera do pewnej wartości maksymalnej, a następnie maleje wykładniczo do zera. Nlosunkowo proste działania matematyczne pozwalają znaleźć 2 wyrażenia pozwalające obliczyć czas, po którym obserwuje się maksymalne stężenie RUbstancji leczniczej w osoczu, oraz wielkość tego stężenia maksymalnego:

^1 1„ *•" ^- k.-K ^ln K	(9.4)
FD K, v Vi	(9.5)

Pozanaczyniowc podawanie lekózo 135