0051

52

I. Teoria granic

podczas gdy wysokość tych graniastosłupów jest jednakowa: H/it. Dlatego

v:--

C    , 2 » QH »(« + l)(2n + l) QH (n + l)(2»> + l)(‘)

—jU +2 +...+H )—=— •---------i-    -

n    n n    6    6    n

czyli

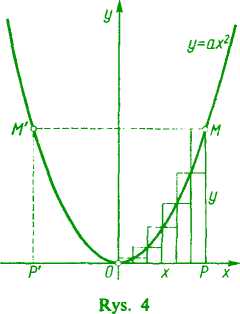
4) Znaleźć pole Q figury O PM, ograniczonej częścią OM paraboli y = ax¹ (a> 0), odcinkiem OP osi Ox i odcinkiem PM (rys. 4).

Podzielmy odcinek OP na n równych części i zbudujmy na nich wpisane i opisane prostokąty. Pola Q„ i Q'„ utworzonych

x

z nich figur schodkowych różnią się o pole —y największego

n

prostokąta. Stąd, jak w przykładzie 3), różnica Q'„—Q„-¹0, a ponieważ

G»<Q<C»,

więc

G=limQ.=limCń.

Ponieważ wysokości oddzielnych prostokątów są rzędnymi punktów paraboli, o odciętych

1

— x, n

■ x,

X,

więc zgodnie z równaniem krzywej rzędne wynoszą odpowiednio 2²    f²

*• o    • i    •»

1 2

a — x , n

^a7^X

ax ,

i dla Q'„ otrzymujemy wyrażenie

G» = —r (l^ł+2² + ...+n²) -

Stąd

ax³ x-ax² xy

e-^|ta«-_T-—-_T-

Korzystając z tego wzoru łatwo otrzymać, że pole wycinka parabolicznego M'OM równa się ~xy, tj. dwum trzecim pola opisanego prostokąta (wynik ten był znany jeszcze Archimedesowi; (²).

5) Dowieść, że przy 0<k<l jest

lim l(n + l)‘-«‘]=0.

n¹

Mamy tu wyrażenie nieoznaczone postaci oo —oo. Przekształcamy badane wyrażenie, wynosząc przed nawias:

Ponieważ 1 /n¹ '¹->0, to również (n+1)¹—n¹-»0, cnd.

1

Wykorzystujemy tutaj znany wzór na sumę kwadratów n pierwszych liczb naturalnych.

(²) Ogólną definicję pola figury krzywoliniowej podamy dopiero w rozdziale X (w tomie drugim), tam właśnie przytoczona tu metoda obliczania pola będzie uogólniona na inne figury krzywoliniowe.