081

81

5.1. Estymacja punktowa

jest estymatorem nieobciążonym parametru a, gdyż

ET_n = - (n (a + 1 /2)) ~ 1 /2 = a. n

Zgodność tego estymatora wynika z prawa wielkich liczb i z faktu, że EX —

a+1/2.

5.1.2. Metoda momentów

Metoda momentów jest jedną z wielu metod konstruowania estymatorów parametrów rozkładu cechy w populacji generalnej. Przyjmijmy, że parametr 9 jest jednoznacznie określony przez wartości pierwszych k momentów teoretycznych cechy. Oznacza to, że

0 = f{m_l,...,m_k).

A

Estymator

otrzymany

metodą

momentów

Estymator 6 parametru 6 otrzymany metodą momentów określa się wzorem

e = f(M_v.

ł

gdzie M_i są empirycznymi odpowiednikami momentów zwykłych m-. W szczególności jeśli parametr 6 jest funkcją tylko pierwszego momentu teoretycznego m, to estymator jest funkcją statystyki X.

Przykład. Niech X ma rozkład jednostajny na odcinku [a,b\. Przyjmijmy, że a — 0 oraz a — b jest nieznanym parametrem tego rozkładu. Ponieważ

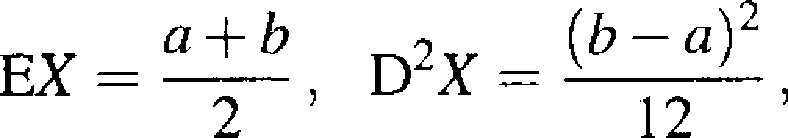
(5.1.1)

to a — 2m, a więc a — 2X. Nie jest to estymator najlepszy, gdyż można spotkać takie dane, że niektóre z nich wyjdą poza prawy koniec tak oszacowanego przedziału. Jeżeli chcemy oszacować oba końce a i b, które nie są znane, to trzeba rozwiązać układ dwóch równań otrzymanych z (5.1.1) obliczając a i b w zależności od m i cr, tzn. a — a(m, cr), b ~ b(m, a). Stąd b — 2m — a oraz a~m — a\/3, a więc d — X — S\/3, b — X -b SyJ3.

Przykład. Dla rozkładu wykładniczego, którego gęstość jest określona wzorem (2.4.1), mamy EX — \)X. Stąd X ~ \/X.

5.1.3. Metoda największej wiarogodności

Idea metody największej wiarogodności polega na oszacowaniu nieznanych parametrów tak, aby empiryczne dane były przy tym oszacowaniu najbardziej