skanuj0011

Slajd

2

.. . .	Hajd	TRANSMITANCJA OPERATOROWA
transformacja Laplace’a (przekształcenie jednostronne dla t>0)	i
f 0 \		Równanie rówiiakowc liniowe . 'd^nX d^2x dx . ... _ ... „ du D d^mu df^n ;: dt^2 dt ° ° ^1 1 df ^m dt^m
s= <x + oj -Haplacean (liczba zespolona)		Warunki początkowe zerowe:
' transformata \		u(0^+) = u"’(()* ) = .... = u^(m,(0+) = O] x(0^+) = x^u>(0* ) = .... = x^,r"((X ) = ()]

fliektóra własności transformaty Laplace'a

Operacja	Oryginał	Transformata
Dodawania		a^F^(s) + a^P^Cs)
Różniczkowanie w dziedzinie czasu	df 35	sP(a) - f(O^ł)
Całkowanie w dziedzinie czasu	Jf (t)dt
Różniczkowanie w dziedzinie zmiennej zespolonej	-t-f(t)	d? <5
Całkowanie w dziedzinie zmiennej zespolonej		i
załatw skali	df)	aP(aa)
Przesunięcie w dziedzinie czasu	f(t-i)
Przesuniecie w dziedzinie częstotliwości	i(t).•-**	?(•+*)
.......Splot-w. dziedzinie ' czasu	fn(t) * f2(t)	r1(s).y2^)

Slajd

3

oznaczając-

L{ u( t }} = (!( s) l{x(t)} = X(s)

otrzymujemy na zasadzie prawa o liniowości i o różniczkowaniu

A„ ■ x" • X(s) + + A₃ ■ s'² ■ X(s) + A, ■ s ■ X(s) + A„ ■ X(s) =

^: = B„ ■ U(s) + B_r s ■ U(s) + B₂ ■ s² ■ U(s) +......+ B_m ■ x^m ■ U(s)

i TiiUbKatuhi ja operatorowa to stosunek transformaty wielkości wyjściowej do transformaty wejściowej, przy zerowych warunkach początkowych

_G(_S) =    ₌ ^Bo^+Br^s +.........+ ^Bm ■ s^m

u(s) A₀+A_rs +.........+ A„ ■ sⁿ

Slajd

4

Hiektóre własności transformaty Laplace* a

Operacja	Oryginał	Transformata
Dodawanie	a1f1{t) ♦	a1»1(a) + aj-PpCs)
Różnicr-kowanle w dziedzinie czasu	df 55	ST(S) - f<0*>
Całkowanie w dziedzinie czasu	Jf(t)dt	il»l t 1 rM)(Q+)
Różniczkowanie w dziedzinie zmiennej zespolonej	-t-f(t)	dP 35
Całkowanie w dziedzinie- zmiennej zespolonej		a
Zmiana skali	*(f)	sP(as)
Przesunięcie w dziedzinie szattu	f(t-t)
Przesuniecie V dziedzinie częstotliwości	*<*>■•-**	P(S+8)
Splot w dziedzinie	fn(t) * f2(t)

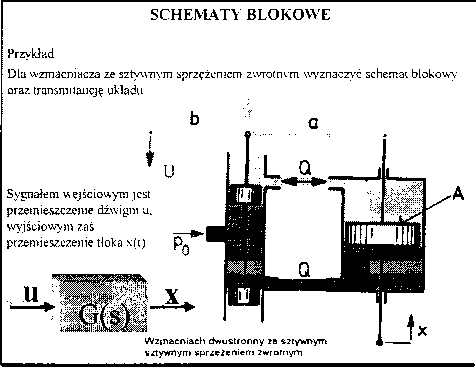
13