Układy równań liniowych6

102

Układy równań liniowych

mniejszy od 4, zaś dodanie czwartego liniowo zależnego równania nie podwyższa tego rzędu do 4.

c) Ceny jednostkowe poszczególnych produktów moglibyśmy wyznaczyć z układu równań o macierzy rzędu 4, np. z układu Cramera. Rząd macierzy układu trzech równań napisanych na początku jest równy

2    2 10 3 1 2 20 1

3    15 2

1		'0 —2	-30	11
^w« --	= rz	1 2	| 20	i
u 3 - 3u-2		0 -5		-i.
J			—55

co zresztą można już było wcześniej wywnioskować na podstawie rachunku przeprowadzonego w punkcie a). Zakup, jakiego powinniśmy dokonać, musiałby się więc składać z ki kostek masła, fc₂ bochenków chleba, jaj i &4 litrów mleka, gdzie fci ^ 1, /c₂    1,

ki ^ 1, ki ^ 1, przy czym musi być spełniony warunek

2	2	10	3
1	2	20	1
3	1	5	2
ki	fc2	ks	/C4

Warunek ten spełniony jest np. dla k\ = 6, /c₂ = 5, k-s — 35, fej = 1. d) Do początkowego układu trzech równań dołączamy czwarte równanie

x + y + z -kt = 3,6.

Rozwiązujemy otrzymany układ czterech równań (metodą „kolumn jednostkowych”)

' 2 2 10 3	9.5 '
1 2 20 1	8.2
3 1 5 2	8.9
.11 11	3.6

<*•1 -.2 U.'3 — 3u.’2 !l>4 — ttj

'0 -2 -30 1 1 2 20 1 0 -5 -55 -1 0 -1 -19    0

-6.9'
8.2	Ki —fei'i
-15.7
-4.6

-6.9'

15.1

-22.6

4.6

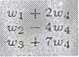
'0 -2 -30 1 1    4    50    0

0 -7 -85 0 0    1    19    0

'0	0	8	1	2.3'
1	0	-26	0	-3.3
0	0	48	0	9.6
.0	1	19	0	4.6.
'0	0	8	1	2.3'
1	0	-26	0	-3.3
0	0	1	0	0.2
0	i	19	0	4.6

'0 0 0 1	0.7'
10 0 0	1.9
0 0 10	0.2
0 10 0	0.8.

Stąd wynika, że czwarty zakup ki = k₂ = k₃ = ki = 1 czym zadość warunkowi z punktu c) i pozwala na wyznaczenie cen jednostkowych (w złotych), które są równe x = 1.9, y = 0.8, z ⁼ 0.2 ii — 0.7.

Przykłady

103

Metody rozwiązywania układów Cramera

• przykład 4.13

Rozwiązać podane układy Cramera metodą eliminacji Gaussa - Jordana:

f x + 5y = 2 ^a> \ -3x + 6y = 15 ’

{x - 2y + 3z — -7 3x + y + Az =    5 ;

2x + 5y + z = 18

x    +    2y    —    3z    =0

Ax    +    Sy    —    7z    +    t    =    1

|    x    +    2 y    —    z    +    t    =    1 ’

[    — x    +    y    +    4.z    +    Gt    =    0

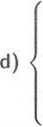
x + 4y    +    2z    -    s    =    3

2x -p 9y    “P    6z    —    2s    —    3t =    5

x + 2 y    -    z    -    s    +    5t=    5

—2x -7y    +    z    +    3s    —    4t =    -5

—x -5y    -    z    +    3s    +    Gt =    4

Rozwiązanie

Metoda eliminacji Gaussa - Jordana dla układu Cramera postaci AX = B polega na rozwiązaniu tego układu poprzez doprowadzenie jego macierzy rozszerzonej [A\B\ do postaci [7iX], gdzie I oznacza macierz jednostkową. Przy przekształceniach stosuje się operacje elementarne na wierszach macierzy rozszerzonej, co schematycznie można przedstawić następująco

I\X)

[A\B\

Ponieważ wszystkie wykonywane operacje przekształcają układ równań na układ mu równoważny, więc wektor X pojawiający się przy końcu postępowania jest szukanym rozwiązaniem układu. Kolejność operacji przy rozwiązywaniu naszych przykładów będzie zgodna z algorytmem Gaussa -Jordana sprowadzenia macierzy nieosobliwej do macierzy jednostkowej.

a) Przekształcamy macierz rozszerzoną danego układu równań otrzymując

1 5 -3 6

2

15

1    5    2

0 21 21

2 '
1	tó i —

1 0 0 1

Ostatni zapis oznacza, że

flx + 0t/=— 3 \ 0 • x + 1 • y =    1 ’

zatem x = -3, y - l.

b) Podobnie rozwiązujemy układ z trzema niewiadomymi

r i	-2	3	-71		r i	-2	3	-7 1		r i	-2	3	-71
3 .2	1	4 1	to 00	U'2 -U’3 - 2u'i	0 .0	7 9	-5	26 32		0	1	5 ~7	26 7
							O			Lo	9	-5	32 J