0277

§ 4. Własności szeregów zbieżnych

279

3) Obliczyć kwadrat:

(*-

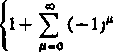
2^2M(/i!)^z

}

2

dowolne).

Wskazówka. Skorzystać z wzoru

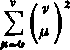
(2v)\ zv 2^2V ■ (»-!)* *

(2#)!

'^jjT > którego dowodzi się elementarnie

Odpowiedź: 1+    (— l)^aw

v-l

4) Tożsamość [patrz 385, 6)J

e

n-0

A_nx

n

oo

^iE‘

lub

E

■•O

a„x" = (1-*)

A„x",

gdzie *4. = <J₀+<łi+ ... +0», dowodzi się łatwo przez pomnożenie szeregów. Jeśli przy tym w przedziale (—R, R) (0<H< 1) jest zbieżny jeden z tych szeregów, wynika stąd już zbieżność w tym przedziale drugiego szeregu.

5) Udowodnić tożsamość (0>O):

(J_ ₊ J_._*_ ₊ ±±._£l_₊ U₁₊JL_JC+U.^+ \ =

\a ⁺ 2    o+2 ⁺ 2-4    o+4 ⁺    \ ⁺ 2 ⁺ 1-2    7

-i[

6) Jak już wiemy [378, 1) (a)], szereg

^|,+Si‘⁺

(0+1) (o+3) (0+2) (0+4)

x²+

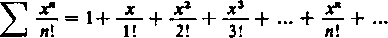
I-O

jest zbieżny bezwzględnie dla wszystkich wartości x. Oznaczymy jego sumę przez E(x).

Zastępując tutaj x przez y otrzymujemy analogiczny szereg o sumie równej E (>•). Iloczyn Cauchy’ego obydwu szeregów ma wyraz ogólny

1.21 +JL nl 1!

y-¹ i x² .    y-²    .

(«-!)!    2!    (#i—2)!    ‘

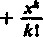
yt-k

(n—k)l

H

-E

1-0

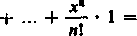
1

k\ (n—k)!

x“ y-*

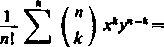
(s+y)"

nl

1-0

Tak więc otrzymujemy dla nie znanej nam na razie funkcji E (*) związek

E{x)-E(y)=*E(x+y)

słuszny dla dowolnych x i y. Później pozwoli nam to ustalić, że E (jc) jest funkcją wykładniczą [439, 3); porównaj też 75,1°].

7) Za pomocą kryterium d’Alemberta łatwo jest stwierdzić, że. szeregi

CM = £(-1)*

(2»)!

= 1 -

2!

+ £1_

4!

+ (-O’-’

(2/i)!

S(x)= £(-l)"-‘

+ ••

y3    1*5

___ _x—-__{- ___4-(— U™-¹

(2m—1)1    3! ⁺ 5!    " ^J