0281

283

§ 4. Własności szeregów zbieżnych

Jeżeli przyjmiemy B_m = B~p_m, gdzie reszta fl_m -*■ 0, gdy »;-►«, to sumę C„ możemy napisać w postaci C, = A. B-y„ gdzie y, =    + ...    jJ₂+a. Pi.

Ponieważ A_n -*■ i4, całe zagadnienie redukuje się do dowodu, że lim y„ = 0. To z kolei wynika od razu z 3 ustępu 391 (dla x_ą = p„ i y„ = a„), jeśli weźmie się pod uwagę, że

|oil + |a₂|+ ... +|a„] < A* ,

gdzie A* jest sumą zbieżnego z założenia szeregu (A*).

Jako przykład zastosowania twierdzenia rozpatrzmy jeszcze raz zadanie 4) z ustępu 390. Wspom-

00

niana tam równość.zachodzi także na końcu x — ±R przedziału zbieżności szeregu 2 a,*", jeżeli R< 1

*-»0

i szereg jest w tym końcu w ogóle zbieżny (chociażby warunkowo).

Zauważmy, że gdyby oba szeregi (A) i (B) były tylko warunkowo zbieżne, to nie można by już ręczyć za zbieżność szeregu (13). Dla przykładu pomnóżmy szereg

yi (-l)"-¹

/«

= 1-

⁺ 7f-- ⁺⁽-^w

+...

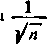
zbieżny — jak wiemy — warunkowo [382, 2)] przez siebie samego. W tym przypadku

c„

(-i r-

--¹ /—L_

li

fń "* /2Yn-l

+ ••• + ■    -,x-r_.    + ... +

yi -yn-i+i    yi

=t)

Każdy ze składników w nawiasie jest większy od 1 /«, wobec czego |c„|>l (dla n>l) i szereg 2 c„ jest

Ił — 1

rozbieżny [364, 5°].

Jeśli jednak postąpimy analogicznie z również warunkowo zbieżnym [(382, 1)] szeregiem

ln 2 =

-ty-¹

= i-4-+ 4--... +(

-i)—*•—-n

to okaże się, że

= (-])"-' f—— + ¹ + ... 4--5—— + ... + —L] =

Ll« 2 («—1)    1 (w—i+1)    wij

-^<-^,)“'4r(¹⁺T⁺-⁺t)-

Tutaj c. dąży do 0 malejąc monotonicznie, gdy n rośnie, a więc na mocy twierdzenia Leibniza [381] szereg

00

£c, będzie jednak zbieżny. Jaka jest suma tego szeregu ? Czy jest równa (ln 2)² ? Na te pytania daje odpo-

II—l

wiedź

Twierdzenie Abela. Jeżeli tylko dla dwóch zbieżnych szeregów (A) i (B) ich iloczyn w postaci Cauchy'ego jest zbieżny, to suma C tego iloczynu jest równa A-B.

Dowód. Zachowujemy poprzednie oznaczenia. Z (16) otrzymujemy łatwo Ci + C₂+ ... +C„ = Ai B_nĄ-A2 B_n-1+ ... Ą-A, Bi .

Podzielmy tę równość stronami przez n i przejdźmy do granicy, gdy n -*■ 00. Ponieważ C_m -*■ C, więc na mocy twierdzenia Cauchy’ego [33, patrz też 391,1°] także i średnia arytmetyczna

Ci C₂ 4~ ... +C» j q

n