0279

281

§ 4. Własności szeregów zbieżnych

Ponieważ m jest tu już ustalone, istnieje — z uwagi na (a) — takie N>m, że dla n>N pierwszy składnik po prawej stronie jest też mniejszy od e/2, a zatem ];r'|<e, c.b.d.o.

II. Niech współczynniki t,_m spełniają oprócz warunków (a) i (b) dodatkowy warunek

(c)    T, = t._x+t.i+ ... +t_m -*■ 1, gdy n -*■ oo (‘).

Wówczas, jeżeli x_R-+ a (a — skończone), to także

Xm = tnl *1 + t_m2 *2 + ... +/.. *»,-*■ a •

Dowód. Wyrażenie dla x' można oczywiście napisać w postaci

x'. = t,_l(x_l-a)+t,₂(x₂—a)+ ... +t„ (x.-a)+T, a .

Stosując twierdzenie I do ciągu x,—a dążącego do zera i opierając się na założeniu (c), otrzymujemy bezpośrednio żądany wniosek.

1° Twierdzenie Cauchy'ego [33] otrzymujemy stąd przyjmując

im 1 = tul —    — t,a = — .

n

Spełnianie warunków (a), (b), (c) jest oczywiste.

2° Przejdźmy do twierdzenia Stolza [33] zachowując dane oznaczenia. Mamy więc dwa ciągi {x„} i {y,}, z których drugi dąży monofonicznie do + oo.

Załóżmy, że

ym-y,-i

a

(n — 1,2,

x₀ = Jo = 0)

i zastosujemy do tego ciągu twierdzenie II przyjmując t._m —    . Spełnianie warunków (a), (b),

(c) łatwo jest sprawdzić. Otrzymujemy wniosek, że

II

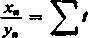
Xm X_m—₂

ym-ym-1

O,

Przytoczymy kilka pożytecznych wniosków z twierdzenia ToepUtza.

3° Niech będą dane dwa ciągi {x„} i {y,} zbieżne do zera, przy czym drugi z ciągów spełnia warunek Ij^,il + |j2l+ ... +|y«l < K (n = 1,2,3,...; K = const) .

Wówczas także

z. = x₂y_m+x₂y_m-_l+ ... +x.y₂ -*-0.

Dowód otrzymuje się przez zwykłe zastosowanie twierdzenia I dla t_mm = J’,_„₊₁.

4° Jeżeli x. -*■ a, y, -*■ b, to

z. = x₁y_m+x₂y.-i + ... -i-Jf.yi _gb n

Niech będzie najpierw a — 0. Należy udowodnić, że z, -* 0. Wynika to wprost z wniosku 3°, jeżeli zastąpi się w nim y, przez yjn. Warunek nakładany tam na y. łatwo jest sprawdzić, jeśli uwzględnimy, że y, jest tu ograniczone, |j'„| < K.

(‘) W zastosowaniach jest zazwyczaj T_m = 1.