027

A HibUl. IM1U.1 ,Vvu r ), buui :uO

ISBN D4H1II ł-7. © l>. »N TOS >«}

2 a SZYBKOŚĆ ROZPADU PROMIENIOTWÓRCZEGO 27

dzcmc to stanowi nieco rozszerzona treść reguły Fajansu i Soddy*ego (1911-1913 r.). Reguła ta w swojej pierwotnej postaci nie obejmowała nieznanej jeszcze wówczas przemiany fi*.

Jadra powstające w wyniku przemian promieniotwórczych mogą być obdarzone niekiedy nadmiarem energii, którego pozbywają się, emitując promieniowanie elektromagnetyczne zwane promieniowaniem y Odznacza się ono jeszcze mniejszą długością fali niż promieniowanie rentgenowskie. Emisji promieniowania y nie towarzyszy zmiana liczby atomowej ani liczby masowej.

2.4. SZYBKOŚĆ ROZPADU PROMIENIOTWÓRCZEGO

Rozpad wszystkich nietrwałych jąder, zarówno naturalnych jak i otrzymanych sztucz nic. przebiega w taki sposób, żc jego szybkość jest w każdej chwili wprost proporcjonalna do liczby jeszcze nie rozłożonych atomów N.

Szybkość tę wyrażamy stosunkiem liczby atomów diV do czasu dr. w którym atomy tc ulegają rozpadowi: mamy więc

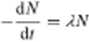
<2.2)

Stała proporcjonalności A nosi nazwę stałej rozpadu promieniotwórczego. Znak minus przed ułamkiem kładziemy z tego względu, żc diV jako liczba przedstawiająca uby tek liczby atomów jest liczbą ujemną, szybkość natomiast musi być wielkością dodatnią.

Po przekształceniu i scalkowamu równania (2.2) otrzymujemy

- In N m X + consi (2.3)

W celu obliczenia stałej całkowania przyjmujemy, że w chwili początkowej, / = 0, liczba atomów danego izotopu wynosiła ,V₀. Po podstawieniu N = N» i I = 0 znajdujemy, żc const = - In N₀ oraz że

In — = -Al (2.4)

A o

czyli

N m No-(2.5)

Na podstawie równania (2.4) możemy obliczyć okres póltrwania T_{,₂, izotopu promieniotwórczego. tj. czas. w którym ulega rozpadowi połowa ilości danego izotopu. Wystarczy bowiem podstawić i — T,_f2 oraz N — No/2, aby otrzymać

T\n = (2.6)

Z równania (2.6) wynika, że okres póltrwania izotopu jest niezależny od jego ilości początkowej. Jest to wielkość używana najczęściej do charakteryzowania szybkości rozpadu promieniotwórczego.