051

A HibUl. IM1U.1 ,Vvu    r ), buui :uO

ISBN D4H1II ł-7. © l>. »N TOS >«}

3 2 ZASADA NIEOZNACZONOŚCI HEISENBEftGA    51

Drogę wyjścia z trudności, jakie wynikają z przyjęcia takiego dualizmu w naturze światła, wskazał francuski fizyk Louis de Broglie. Według hipotezy de Broglie‘a ruch fotonów oraz takich cząsick elementarnych, jak elektrony, protony, neutrony, w pewnych warunkach musi być opisywany jako ruch korpuskuły. cząstki o określonej masie, w innych natomiast — wyłącznic jako ruch fali. Cząstce o masie m. równoważnej energii E = mc², poruszającej się z prędkością u przypisuje się falę (nazwiemy ją falą dc Broglic'a) o długości:

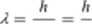
mu p

podobnie jak, zgodnie z równaniem (3.8), fotonowi przypisuje się falę o długości

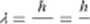
mc p

Pęd fotonów, wykazujących wprawdzie ogromną prędkość, lecz bardzo małą masę. jest z reguły mniejszy niż pęd elektronów, które poruszają się z prędkościami wielokrotnie mniejszymi niż światło, mają jednak dużą masę w porównaniu z masą fotonów. W rezultacie fotonom odpowiadają znacznie większe długości fali niż elektronom. To jest właśnie powodem, żc w przypadku fotonów łatwiej dostrzega się ich właściwości falowe, w przypadku elektronów natomiast — ich właściwości korpuskularne. Jak widzieliśmy, zjawiska, w których przejawia się falowy charakter światła: załamanie, dyfrakcja. interferencja itd.. zostały poznane znacznie wcześniej niz efekt fotoclcktryczny i zjawisko Comptona, w któiych w typowy sposób pizejawia się charakter korpuskularny światła. W przypadku elektronów, protonów czy cząstek u poznano najpierw ich właściwości korpuskularne. np wyznaczając dla nich stosunek ładunku do masy <p 13). Odkrycie ich właściwości falowych nastąpiło dopiero po pracach de Broglie’a i stało się potwierdzeniem jego poglądów W roku 1927 Clinton J. Davisson i 1-ester II Gernier stwierdzili mianowicie występowanie dyfrakcji elektronów, polegającej na tym. że strumień rozpędzonych elektronów, przechodząc przez bardzo cienkie warstwy substancji krystalicznych, ulega rozszczepieniu na kilka promieni, podobnie jak światło ulega dyfrakcji. przechodząc przez siatkę dyfrakcyjną, funkcję siatki dyfrakcyjnej spełnia w tym pizypadku sieć przestrzenna kryształu. Dyfrakcja elektronów na cienkich warstwach krystalicznych wykazuje wiele podobieństw do dyfrakcji promieni rentgenowskich na kryształach (p. 7.5). Zjawisko dyfrakcji na kryształach występuje także w przypadku strumieni protonów, cząstek u i neutronów. Wszystkie te fakty powodują, żc hipotezę de Broglie'a uważamy za potwierdzoną przez doświadczenie, a konsekwencje jej — jak zobaczymy w następnych paragrafach — uwzględniamy, opisując zachowanie się elektronów w atomie.

3.2. ZASADA NIEOZNACZONOŚCI HEISENBERGA

W mechanice klasycznej zajmującej się ruchem ciał makroskopowych, tj. ciał bardzo dużych w porównaniu z rozmiarami atomów, można dla każdego ciała wyznaczyć