054

A HibUl. IM1U.1 .Vvu    r ), buui :uO

ISBN D4H1II ł-7. © l>. »N TOS >«}

54

3 ELEKTRONOWA STRUKTURA ATOMU

wych opisuje mechanika klasyczna, w której można podać równocześnie pęd i położenie ciała Opisem mchu cząstek elementarnych zajmuje się mechanika kwantowa Opisuje ona układy, przy których rozpatrywaniu musi być uwzględniona zasada nieoznaczoności Heisenberga, dopuszczająca dokładne oznaczenie położenia cząstki tylko przy równoczesnej rezygnacji z oznaczenia jej pędu. lub odwrotnie: dokładne oznaczenie pędu i rezygnację ze znajomości dokładnego położenia. Układ złożony z pewnej liczby cząstek możemy więc opisywać bądź posługując się współrzędnymi określającymi położenie, bądź też. wprowadzając do rozważań tylko pędy W pierwszym przypadku mówimy o opisie w przedstawieniu współrzędnych, w drugim — opisie w przedstawieniu pędów. W dalszych rozważaniach będziemy posługiwać się tylko pierwszym z wymienionych sposobów.

Podkreślić należy, że opisując układ w przedstawieniu współrzędnych, na ogół określamy współrzędne tylko z pewnym przybliżeniem, np. współrzędną .v określamy z dokładnością do Aa. Podobnie opisując układ w przedstawieniu pędów, określamy pęd cząstki tylko z dokładnością do A/>. Oznacza to. że współrzędne w przedstawieniu współrzędnych i pędy w przedstawieniu pędów określamy tylko z pewnym prawdopodobieństwem.

W rezultacie mechanika kwantowa zamiast określać ostro położenie cząstki (określać ostro jej współrzędne), zakłada istnienie określonego prawdopodobieństwa napotkania cząstki w danym miejscu w przestrzeni. Oznaczmy symbolem W prawdopodobieństwo znalezienia cząstki w objętości dr (w elemencie przestrzeni dr). Stosunek M'/dr nazywamy gęstością prawdopodobieństwa napotkania cząstki. Tę wielkość będziemy ozna-

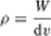
Prawdopodobieństwo W = pdv napotkania cząstki jest naturalnie różne w różnych miejscach. Oznacza to. ze również i gęstość prawdopodobieństwa jest zależna od miejsca Możemy ją przeto wyrazić jako funkcję współrzędnych x.y,z:

(3.14)

p = pix. y. z)

Skala, w jakiej wyraża się prawdopodobieństwo pdv. dobrana jest w laki sposób, że prawdopodobieństwo równe 1 oznacza pewność znalezienia cząstki w danej objętości, a prawdopodobieństwo równe 0 — pewność, że cząstki tam nic ma. Jeśli więc cząstka w ogóle się pojawia w układzie współrzędnych a . y. z, to całka prawdopodobieństwa napotkania cząstki w elemencie przestrzeni dr rozciągnięta na całą przestrzeń wynosi 1:

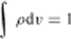
(3.15>

3.3. FUNKCJE FALOWE I RÓWNANIE SCHRÓDINGERA

W poprzednim paragrafie stwierdzono, że mechanika kwantowa, chcąc dać poprawny, zgodny z doświadczeniem, opis ruchu cząstek elementarnych, rezygnuje z określania