0309

311

§ 6. Iloczyny nieskończone

Zakończyliśmy wreszcie badanie zbieżności szeregu hipergeometrycznego .Wyniki możemy zestawić w tabeli:

W<1		bezwzględnie zbieżny
W>1		rozbieżny
	y — ac — P> 0	bezwzględnie zbieżny
X = 1	y-<x-jS<0	rozbieżny
	y—<x—fi>0	bezwzględnie zbieżny
X = -1	0>y —a —/S> —1	warunkowo zbieżny
	y—a —/3< —1	rozbieżny

9) Udowodnić, że szereg

£ a„(x²— 1) (x²—2¹) ... (x²-n²)

»»1

jest zbieżny dla wszystkich wartości x, jeżeli tylko jest zbieżny dla danej niecałkowitej wartości x = x₀ (T. Stirling).

Wyrazy tego szeregu różnią się od wyrazów zbieżnego szeregu

<x>

oAxo-l) (xi-2²) ... (xl-n²)

•-i

czynnikami

(x² — 1)(x²—2²) ,..(x²-n²)

(xo~l) (Xq — 2²) ... (.r„—»²) '

które dla dostatecznie dużych /» zmieniają się monotonicznie wraz z n.

Pozostaje jeszcze wykazać, że są ograniczone, bo wtedy można będzie zastosować kryterium Abela. W tym celu najprościej bedzie przekonać się, że jest zbieżny iloczyn nieskończony

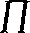
x²-n²

Pozostawiamy to czytelnikowi.

10) Rozpatrzmy (ża Eulerem) iloczyn nieskończony

(13)

r(A)

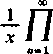
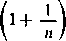
1+ — n

X

zakładając, że x jest różne od zera i od liczb całkowitych ujemnych. Łatwo przedstawić ogólny czynnik tego iloczynu w postaci

1+ —

n

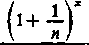
i ,    *(*-!)

2n²