0329

331

§ 8. Rachunki przybliżone — Przekształcanie szeregów

skąd łatwo można obliczyć logi₀3. Podstawiając dalej we wzorze (2) n = 2400 = 3 • 2³•10² mamy 7i+1 = 2401 = 7⁴, zatem

4 logio 7 — 3 logio 2 —logio 3 — 2

™-(i+±--1-+ JL--1_

4801 \    3    23049601    5    23049601² skąd znajdziemy logi₀7. Dobierając odpowiednie kombinacje liczb można znaleźć z dowolną dokładnością logarytmy liczb pierwszych, a z nich, za pomocą mnożenia przez liczby naturalne i dodawania, obliczyć logarytmy liczb złożonych.

Można by też postąpić inaczej: obliczać bezpośrednio logarytmy kolejnych liczb naturalnych przechodząc od logion do logio (n+1) na podstawie wzoru (2). Na przykład od obliczenia logarytmów liczb od 1000 do 10000 weźmiemy we wzorze (2) tylko jeden wyraz, tzn. przyjmiemy w przybliżeniu

log,₀(n+1) logio n = - ^2A/,    (10³ < n < 10⁴).

2n+l

Błąd wyniesie przy tym

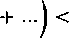
_!__,J___!_

2n+1 \ 3    (2n+l)² ' 5    (2n+l)⁴

< — ²m— (i₊ _*._ +—l_₊v--m_

3(2n+l)³ \    (2#i+l)²    (2/7+1)⁴    /    3 (2n+l)-2n-(2n+2)    24n³

Ponieważ w naszym wypadku jest n > 10³, a 2M< 1, więc

a < -!-<    ¹    .

24-10*    2-10¹⁰

Gdyby się nawet wszystkie błędy dodawały, to w sumie błąd byłby mniejszy niż 10⁴/2 • 10¹⁰ = = y • 10~⁶. Łatwo jednak uniknąć takiego spiętrzenia błędów, obliczając pierwszą metodą pewną liczbę logarytmów kontrolnych. W ten sposób można osiągnąć znacznie większą dokładność zachowując równocześnie charakterystyczny dla drugiej metody automatyzm obliczeń, co jest szczególnie cenne przy obliczaniu obszernych tablic.

412. Obliczanie pierwiastków. Najprościej jest obliczyć pierwiastki za pomocą tablicy logarytmów. Jeżeli jednak potrzebne są poszczególne pierwiastki z bardzo dużą dokładnością, to warto sięgnąć do szeregu dwumiennego [407, (22)]

m (771 — 1) 1-2

*² +

(1 +X)" = 1+771JC +

771 (771- 1) (771-2)    , ,

1-2-3    ⁺

wartość a tego pierwiastka,

Przypuśćmy, że trzeba obliczyć |[a, przy czym znana jest już przybliżona ale trzeba zwiększyć dokładność. Jeśli przyjmiemy

Ar = 1+*.

gdzie 1x1 jest niewielką liczbą mniejszą od jedności, to można pierwiastek przekształcić w sposób następujący:

^A = a-^S/a* = a-(l+x)^l/*

i skorzystać z wzoru dwumiennego dla m= 1 jk. Czasem wygodniej jest wychodzić od równości

a*

l+x',