172

A HibUl. IM1U.1 .Vv»i --u, r ), buui :uO
ISBN D4H1II ł-7. © l>. »N TOS >«}
172
x’ = JT + Oy + Oz E y = Oa + y + (Iz z’ = 0.v + Oy + 2
5 SYMETRIA CZĄSTEC2EK
a ' =x cos 2jt/3 - y sin 2jt/3 + Oz Ci y =.t sin 2n/3 + y cos 2n/3 + Or z' = Oa + Oy + z
x' = x + Oy + 0; <Tt. y = O a - y + Oz
Z = Oa + Oy + Z
Macierze, odpowiadające poszczególnym operacjom, nazywamy reprezentacjami tych operacji, a zbiór macierzy odpowiadających wszystkim operacjom danej punktowej grupy symetrii reprezentacją grupy Znając reprezentację, możemy dogodnie dokonywać operacji symetrii na najrozmaitszych obiektach, między innymi na wektorach i na funkcjach. W grę wchodzą tutaj zarówno obiekty o symetrii odpowiadającej danej grupie, jak i obiekty, które takiej symetrii nie wykazują. Obiekty, na których dokonuje się operacji zanotowanych w formie reprezentacji, nazywamy bazą reprezentacji
W omówionym dopiero co przykładzie przekształceń współrzędnych v. y, z punktu P bazę reprezentacji stanowiły wektory składowe x.y. z wektora OP (rys. 5.14b) dane odcinkami OX. OY oraz. OZ
|
F, |
c4 |
C2 |
|
a’ = a + Oy |
a’ = Oa + y |
a' = -a + Oy |
|
y' = Oa + y |
II 1 ir 1 o |
y = Oa + y |
|
[ 1 Ol |
fon |
r-i °i |
|
[o ij |
L-i |
L 0 -u |
O,i
a’ = Oa + y y = a + Oy
Przy rozpatrywaniu tych przekształceń musimy zwrócić uwagę na różnice w zachowaniu się wektora z w porównaniu z wektorami x i y. Wartość i kierunek pierwszego z nich pozostają nie zmienione w toku wszystkich operacji symetrii charakterystycznych dla grupy CĄ,. Znaki wektorów x i y ulegają równoczesnej zmianie. Tc dwa ostatnie wektory w większości operacji wymieniają się między sobą (ewentualnie z równoczesną zmianą znaku), przy czym dzieje się to niezależnie od wektora z. W rezultacie można rozpatrywać niezależnie od siebie transformację równoczesną wektorów x i y oraz transformację wektora z W pierwszym przypadku będziemy mieć następujący układ równań t macierzy:
ov
' [? i]
x'= x + 0.v > ' = 0 a- y
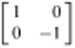
Wyszukiwarka
Podobne podstrony:
A HibUl. IM1U.1 ,Vv»« rw, r ), buui :uO ISBN D4H1II ł-7. © l>. »N TOS >«} 18
A HibUl. IM1U.1 ,Vv»« raa, r ), buui :uO ISBN D4H1II ł-7. © t>< WN TOS >«
A HibUl. IM1U.1 ,Vv»« :i>, r ), buui :uO ISBN D4H1II ł-7. © l>. »N TOS >«
A HibUl. IM1U.1 .Vv»« r ), buui :uO ISBN D4H1II ł-7. © l>. »N TOS >*} 6
A HibUl. IM1U.1 ,Vv»« :u, r ), buui :uO ISBN D4H1II ł-7. © l>. »N TOS >«} 1
A HibUl. IM1U.1 ,Vv». r ), buui :uO ISBN D4H1II t-7. © l>. »N TOS >*} 22 2 J
A HibUl. IM1U.1 ,Vv». -u, r ), buui :uO ISBN D4H1II ł-7. © l>. »N TOS >«} 26
A HibUl. IM1U.1 ,Vv»« .«»•»». :u, r ), buui :uO ISBN D4H1II ł-7. © l>. »N TOS >«} 33 2 7 PROST
A HibUl. IM1U.1 ,Vv»« --u, r ), buui :uO ISBN D4H1II ł-7. © l>. »N TOS »*} 2 JĄ
A HibUl. IM1U.1 ,Vv»« --u, r ), buui :uO ISBN D4H1II ł-7. © l>. »N TOS >«} 3
A HibUl. IM1U.1 ,Vv»« r„, r ), buui :uO ISBN D4H1II ł-7. © l>. »N TOS »*} 44
A HibUl. IM1U.1 ,Vv»« r ), buui :uO ISBN D4H1II f- © l>. »N TOS >«} 50 3
A HibUl. IM1U.1 ,Vv». -u, r ), buui :uO ISBN D4H1II ł-7. © l>. »N TOS >«} S5
A HibUl. IM1U.1 .Vv»« r ), buui :uO ISBN D4H1II ł-7. © l>. »N TOS >«} 59 3 4
A HibUl. IM1U.1 ,Vv»« r„, r ), buui :uO ISBN D4H1II ł-7. © l>. »N TOS >*} 62
A HibUl. IM1U.1 ,Vv»« --u, r ), buui :uO ISBN D4H1II ł-7. © l>. »N TOS >*} 6
A HibUl. IM1U.1 .Vv»« r ), buui :uO ISBN D4H1II ł-7. © l>. »N TOS >«} 3 ELEK
A HibUl. IM1U.1 ,Vv»« r ), buui :uO ISBN D4H1II ł-7. © l>. »N TOS >«} 74 3
więcej podobnych podstron