288

A HibUl. IM1U.1 .Vv»i    r.,, r ), buui :uO

ISBN D4H1II ł-7. © l>. »N TOS »*}

2 aa

9 TERMOCHEMIA

Funkcję, która ma laką właściwość, nazywamy funkcją stanu Energia wewnętrzna jest więc funkcją stanu.

Energia całkowita układu, a więc jego energia wewnętrzna, zmienia się na skutek wymiany ciepła i pracy z otoczeniem. Możemy więc napisać

&U=q + w    <9.2>

Przyjmujemy przy tym. że zarówno ciepło z/ dostarczone do układu, jak i pracę dostarczoną do układu liczymy jako dodatnie, ciepło i pracę oddane przez układ jako ujemne.

Pomimo że zmiana energii wewnętrznej. A i/, zależy tylko od stanu początkowego i końcowego danego układu, wymiana ciepła ani wymiana pracy z otoczeniem takiej właściwości nie wykazują. (XI drogi nic zależy tylko suma obu wielkości, każda z nich z osobna zmienia się zależnie od sposobu, w jaki zostaje przeprowadzona dana przemiana.

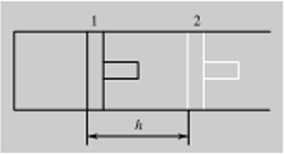
K)S. 9.1. Pr/oiińj cylindra z. tłukiem w poto/emu początkowym 0) i »' położeniu końcowym (2)

Jako przykład możemy rozważyć pracę mechaniczną wykonaną przez układ zawierający n moli cząsteczek gazu doskonałego przy jego izotermicznej i T — const) ekspansji od objętości t>, do objętości is, przeprowadzonej w sposób nieodwracalny i porównać ją z pracą wykonaną przy ekspansji od t>i do vj w sposób odwracalny, Nieodwracalną ekspansję gazu przeprowadzimy w cylindrze o przekroju A. w którym porusza się tłok mc wykazujący praktycznie żadnego tarcia (rys. 9 1). Otoczenie wywiera — w tym przykładzie — na tłok stałe ciśnienie, wynoszące p_mn. Ciśnienie wewnątrz cylindra musi być wyższe od ciśnienia zewnętrznego, gdyż. w przeciwnym razie tłok nic mógłby się poruszać. Dla obliczeń w tym przypadku szczegółowa wartość ciśnienia wewnętrznego, i, > /v„,. nic ma znaczenia, gdyż nasz układ pracując musi pokonać określone ciśnienie zewnętrzne. Siła. którą musi pokonać tłok, wynosi A p_mn. W czasie ekspansji gazu od objętości V\ do objętości tłok przesuwa się o odcinek h. Praca wykonana przez układ przy zachowaniu stałego ciśnienia zewnętrznego wynosi

u> = —hAptftn

Iloczyn hA przedstawia przyrost objętości ekspandującego gazu At' — t'₂ - t>,. Możemy więc napisać

' ^S y    * =    v    (9.3>

W układzie współrzędnych ciśnienie-objętość wartość pracy w przedstawia powierzchnia szara na rys. 9.2a. Przemianę tę nazywamy przemianą nieodwracalną z tego powodu. że gdybyśmy zapragnęli ją odwrócić i skomprymować gaz z powrotem do objęto