Image0111 BMP

I stąd

K-

uA„

II 1

C'-)

, x„lr nby /| J„ lv„) ■/.! , ch ■■    cli

a    f

i,...

iozwi;)7;inie omawianego zagadnienia przedstawia zatem w/ór

i z

J'i, na'

21

+

nhy

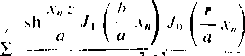
di

O -

)o wyznaczenia stałej P₀ potrzebny jest dodatkowy warunek. Żądając nu przykład, aby F(r, z) równało ię zeru dla z = 0, otrzymuje się V₍, — 0.

1.2.3. Równanie Poissona

Sposób postępowania w przypadku równania Poissona przedstawi my na przykładzie.

Płytka metalowa o postaci prostokąta (rys. 11.1) umieszczona jest w harmonicznym tolu magnetycznym. Niech /i„(v, r) oznacza składową normalną indukcji magnetycznej czględem tej płytki. zaś g i y — jej grubość i kondukty wn ość. Przyjmujemy, że B ( v, i ) :st funkcją parzy,sta względem zmiennych .v, r.

W punkcie 9.6 udowodniliśmy, że wyznaczenie prądów wirowych w rozpatrywanej ■tytce sprowadza się do znalezienia funkcji it(x, ,r) będącej rozwiązaniem równania Pois-ana

v²n <'² u

_--s + -,=J(i)ygB₀(x, y)    (11,46)

ca" óe“

spełniającej warunki brzegowe

«(<!, v)^h(— a, y)~0,    —b<y<b,

u{.x. h) = u (.y , —b)-0,    — a < x < a.

W celu rozwiązania tego zagadnienia wyznaczymy wartości własne i funkcje własne jwnania

6²v dx²

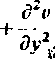
+ Ac = 0

(11.48)

■zy spełnieniu warunków brzegowych

(IL49)

r(«, jO = r(-n,>’) = O_ł -b<y<b, v(x, b) = o(x, — b) — 0,    —a<x<a.

Przypuśćmy, że rozwiązaniem równania (J 1.48) jest v(x, y) = X_k(.x) Y_m(y). Po pod-iwieniu tego wyrażenia do równania (11.48), otrzymujemy

**(*> Y_m(y) + X_k(x) C(y) + AX_k(x) Y_m(y)=0,

czyli

™₊**W_+A.₀.

X_k(x) Y_m(y)

(11.50)

Jeżeli funkcje X_k(x) oraz Y_m(y) są rozwiązaniami równań różniczkowych zwyczajnych

■^/(•^X)+^VŁ-^fc(^) = 0,    ^    ^ j

YZ(y)+i£YJy)=o,

to Spełnione jest równanie (11.50) pod warunkiem, że 2 = A_t„= vjj+^-Rozwiązaniami ogólnymi równań różniczkowych (11.51) są funkcje:

2fit(jc)=a_k cos v_k x + b_k sin v_kx,

YJ,y) = Cm cos fi_my + d_m sin fi_my.

Symetria zagadnienia wymaga parzystości funkcji X_k(.c) oraz Y_m(y), co uzyskuje się przez przyjęcie ń_t=0 oraz d_M=*0, wobec czego

Af_Ł(Jc)=0tCosv_tx,    (11.52)

Y_m(y)=c_m cos n„y.

Podstawiając x=±a do pierwszego równania, zaś y— ±6 do drugiego równania, otrzymujemy (por. wzór (11.47))

a stąd

czyn

COS V_k <3 = 0,

cos/i_mb=0,

vka=(2fc-L)	k = 1,2,
. Jt	m = l, 2,
fimb=(2m-l)
(2fc—l)it ^Vk~ 2 a '	fc-1,2...
(2nx — l)lt	m=l, 2,..
^ 2 b ’

(11.53)

Wartości własne rozpatrywanego zagadnienia wynoszą

(11.54)

(11.55)

4»=^vk+l4. fc, m = l, 2,...,

a funkcje własne przybierają postać

»fan(* - y)=COS v_k X cos n_m y,

gdzie: v_k oraz (i_M określone są przez wzory (11.53). Ciąg funkcyjny {cos v_kx cos fi_my\ jest ciągiem ortogonalnym, a kwadrat jego normy wynosi

a b

iK«||²= I f cos² v_kx cos¹ ą_mydxdy=ab.

-tf -fi

I