Image0113 BMP

Przekształcenie funkcji impulsowej Diraca <5(jt-r) przedstawia wzór

(11.65)

.r{ó(x-T)}= f ó(x-T)e'^i,w:dz=e^J“^r

►trzymany na podstawie zależności (11.64). Inne własności przekształcenia Fouriera ►mówione są w t. I, rozdz. 22.

1.3,2. Pole ładunku punktowego umieszczonego wc wnętrzu rury metalowej

Na osi nieskończenie długiej rury metalowej o promieniu r₀ umieszczony jest ładunek moktowy q (rys. 11.3), Wprowadzamy układ współrzędnych walcowych z, 0, z, którego >ś Oz pokrywa się z osią rury, a ładunek punktowy znajduje się w początku 0 układu współrzędnych. Wyznaczymy potencjał V pola elektrostatycznego we wnętrzu rury. Ze

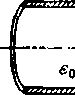
q 2r_g

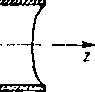
Rys. 11.3. Ładunek punktowy we wnętrzu nieskończenie długiej rury metalowej

względu na symetrię badanego układu, potencjał V nie zależy od współrzędnej 0, wobec czego jest funkcją dwóch zmiennych r, z. Potencjał V(r, z) spełnia równanie Laplace'a

czyli

d²v 1 dv d*V

₊ _ ₊

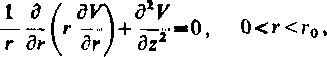
r dr dz²

(11.66)

w każdym punkcie wewnątrz rury, z wyjątkiem początku 0 układu współrzędnych, gdzie znajduje się ładunek q. Warunek brzegowy przybiera postać

K(r₀, z) = 0,

(11.67)

bowiem potencjał ściany metalowej rury jest równy zeru.

Potencjał V(r, z) przedstawiamy w postaci sumy

V(r,z) = V°(r,z) + VXr,z),

(11.68)

gdzie:

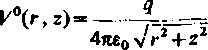
(11.69)

jest potencjałem wytworzonym przez ładunek punktowy q w nieograniczonym środowisku o przeuikalności elektrycznej e_a. Funkcja l⁷⁰(r, z) spełnia równanie Laplace'a

(11.66), wobec czego funkcja V'(r_ti) musi również spełniać to równanie, czyli

(11.70)

d²V 1 dV 0²V^! a?'⁺Tar⁺l? '

Rozpatrywane zagadnienie rozwiążemy przy zastosowaniu przekształcenia Fouriera w odniesieniu do zmiennej z. Transformatę funkcji V"(r, z) przedstawia wzór

+ OD

PV,®)=-*^r{F'(r,z)}= J P'(r, z)e^_J<l’*dz.    (11.71)

— 00

Przekształcając wyraz po wyrazie równania (11.70) za pomocą transformacji Fouriera, mamy

(d²V' 1    1    <dV') (d²F'l

^ 1^'J ⁺ r ^ ITr j ⁺ ^    ° ‘

ai 1/'

Przy założeniu, że dopuszczalna jest zamiana kolejności operacji różniczkowania i całkowania, mamy

(d²F'l d² [arj dr’

lt>V

'{V(r,z)},

a ponadto

(jcu)²^{r(r,z)},

zgodnie ze wzorem (11.63). W wyniku otrzymujemy równanie Bcssela

d ²V'    1 dP'

+ — . . — o)²y'(r, z) = 0, dr r dr

którego rozwiązanie jest (por. p. 12.3) następujące:

V’(r, w) = Al₀(£or) + BK₀(a>r),

gdzie: (₀(x), K₀ (■*) są zmodyfikowanymi funkcjami Bessela rzędu zerowego, pierwszego i drugiego rodzaju, zaś A, B są stałymi. W celu otrzymania rozwiązania skończonego dla r=0, należy przyjąć B=0, bowiem |A"₀(o>r-)j—>oc dla r->0; mamy zatem

V'(r,Q})=AI₀(eor).    (11.72)

Obliczamy obecnie transformatę funkcji V°(r, ż); otrzymujemy

+ ot?

4ne0 .	-- dz = 1 Vr^2 + z^2 00
	■+• 00	+ GO
^9 f	" r -^c-^os(u2	f sin caz
47te0l	J yjr^2A-z^2	’J V?+?

- co