s2 zad12 s2

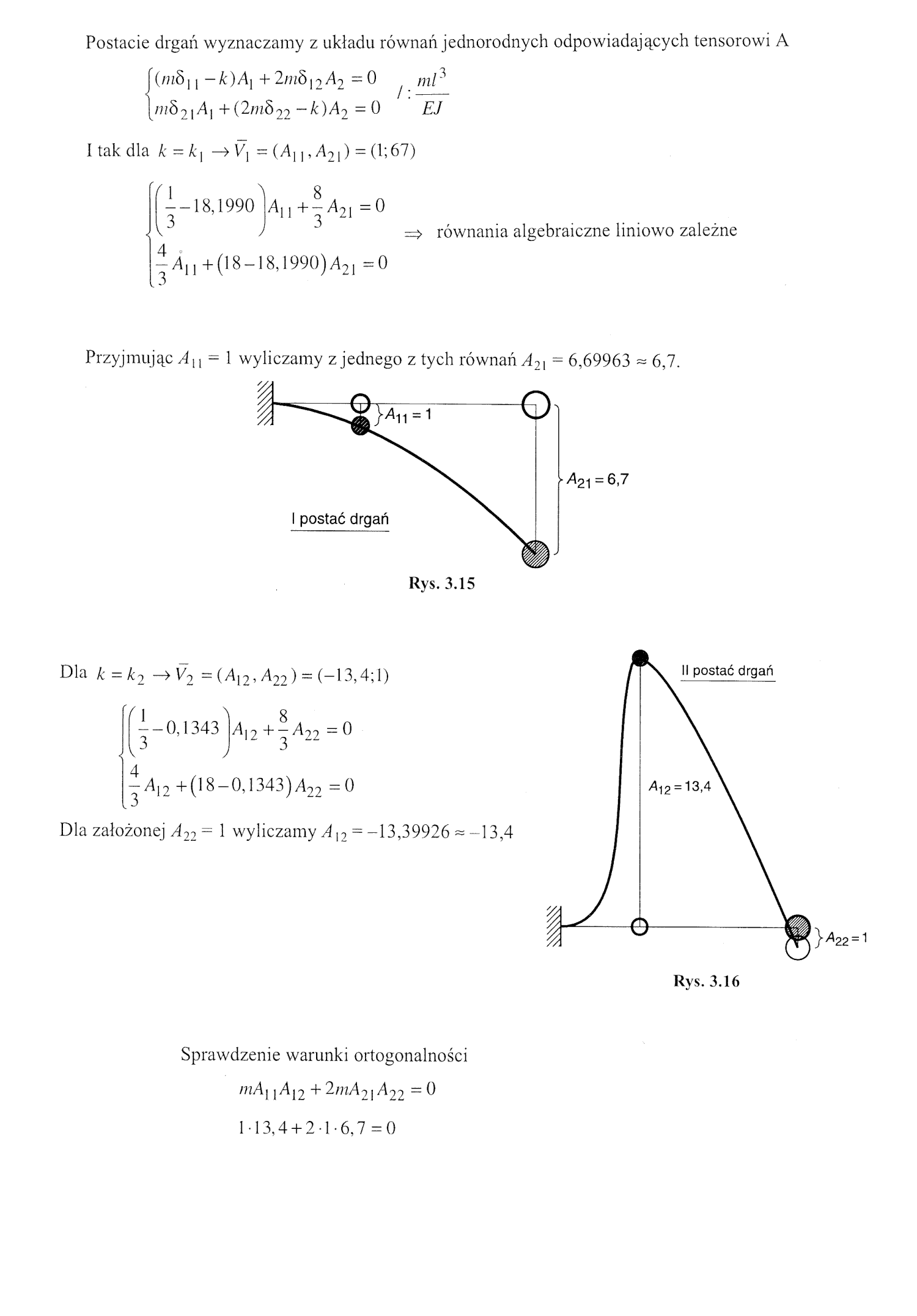
Postacie drgań wyznaczamy z układu równań jednorodnych odpowiadających tensorowi A f(m8] | —k)A\ + 2m6|₂A₂ ⁼ ^

{/7/5₂₁A, +(2m8₂₂ -*)A₂ = 0 ' "&T

Itak dla *==*, -»Vj = (A, ,, A_2l) = (1;67)

1-18,1990^,, +|a₂₁ =0

J    równania algebraiczne liniowo zależne

~ 4_n + (18-18,1990)/t₂₁ =0

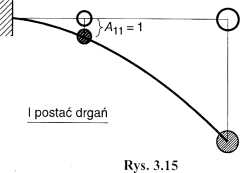
Przyjmując A_u = \ wyliczamy z jednego z tych równań A_2I = 6,69963 = 6,7.

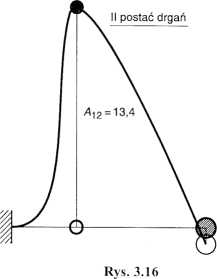
Dla k=k₂ ->V₂ =(,4|₂,A₂₂) = (-13.4;1) ^1-0,1343^,2+^22=0 jA_[2 +(18-0,1343) A₂₂ =0

Dla założonej A₂₂ = 1 wyliczamy A _n = -13,39926 = 13,4

Sprawdzenie warunki ortogonalności m,4| ] ,41 ^ + —iiiA1    =0

I -13,4 + 2 -1 - 6,7 = 0