448 (9)

448 _ 12. Prądy i elektromagnetyczny moment obrotowy maszyny indukcyjnej

wyznacznik układu równań napięciowych

R,(X_m+X^)+j(X_m+XjT (12.4a)

— współczynnik rozproszenia Heylanda całkowity⁰

r =    (12.4b)

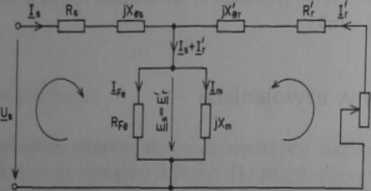
Rys. 12.1. Schemal zastępczy maszyny indukcyjnej symetrycznej

— współczynniki rozproszenia częściowe: a) uzwojenia stojana

x_m+x„

X.

(12.4c)

b) uzwojenia wirnika

X_m+X'„ ' X_a

(12.4d)

pozostałe oznaczenia w zależnościach (12.1)-r(12.3) — jak na rys. 12.1, przy czym indeks „prim” dotyczy parametrów fazowego uzwojenia wirnika sprowadzonych do uzwojenia stojana wg zależności (10.156a); X„, X'„ — reaktancje rozproszeniowe fazowego uzwojenia stojana oraz wirnika sprowadzona do uzwojenia stojana, obliczone wg zależności podanych w p. 10.3.2 oraz 10.3.3; s — poślizg.

W przypadku uzwojeń stojana lub wirnika, w których występują straty dodatkowe na skutek wypierania prądu należy do podanych zależności wstawić rezystancje przemiennoprądowe.

" Podany przez Heylanda wzór ma postać | jg t,+T,+T,t„ a więc inną niż zależność (12.4b). Różnica wynika z inaczej, niż wzorami (12-4c) i (12.4d), zdefiniowanych współczynników

x

rozproszenia r_a oraz x_f. Hey land przyjął t_g * oraz x_r >

X'

* Sposób wyrażania współczyn-

ników rozproszenia zmieniono głównie w celu uproszczenia zapisu wzorów. Zmniejsza się przy tym zapisie również liczba operacji obliczeniowych.

Trudność w posługiwaniu się zależnościami (12.1)-^(12.4) polega nie na ich złożoności, lecz na tym, że reaktancja główna X_m oraz reaktancje rozproszeniowe X„ i X'„ nie są takie same dla wszystkich wartości poślizgu s — zależą bowiem od prądów /, i l'_r oraz od sem E,. Dokładne wartości prądów maszyny w zakresie poślizgów |s| > s„, przy czym s„ — poślizg przy obciążeniu znamionowym, można obliczyć tylko metodą iteracyjną. W pierwszym przybliżeniu, dla zadanego poślizgu s wyznacza się prądy w założeniu, że obwód magnetyczny jest nienasycony obliczając reaktancję główną wg wzoru (10.149). Na podstawie tak wyznaczonego prądu 1, oblicza się sem E, z zależności (7.9) albo wg wzoru

E. = (U,-I,_c,R,-I,„X_a,)²    (12.5)

przy czym:    — prądy wg zależności (12.1a) oraz (lllb).

Na podstawie sem E, oblicza się strumień główny, sumę napięć magnetycznych w obwodzie magnetycznym oraz prąd magnesujący l_m wg zależności (9.78). Z zależności zaś (9.80) oblicza się skorygowaną wartość reaktancji głównej następnej iteracji z uwzględnieniem stopnia nasycenia obwodu magnetycznego. Znając współczynnik nasycenia k, w każdej iteracji obliczeniowej, można wg wskazówek podanych w p. 10.3.8 — obliczyć reaktancje rozproszeniowe z uwzględnieniem napięć magnetycznych w rdzeniu. Obliczenia można zakończyć, jeśli wartości prądu /, otrzymane w dwóch kolejnych iteracjach nie różnią się o więcej niż to wynika z postulowanej dokładności, np. o 0,5% wartości prądu wyznaczonego w ostatniej iteracji. Liczba iteracji koniecznych do uzyskania wymaganej dokładności jest zwykle tym większa, im większy od zera jest poślizg |s|. Bowiem w maszynach małej, jak i dużej mocy, wraz ze zwiększeniem poślizgu powyżej wartości znamionowej, sem E, szybko zmniejsza się, malejąc w stanie do zwarcia — tj. przy poślizgu s = 1 — w przybliżeniu do połowy wartości napięcia, rys. \12.

W wyprowadzeniu wzoru (12.1a) na składową czynną prądu stojana /,_CJ nie uwzględniono strat mocy w rdzeniu oraz strat mechanicznych. Wszyst-

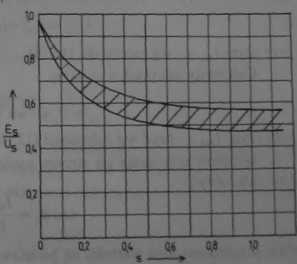
Ry*. 1X2. Obszar zmian względnej wartości sem BJU, w zależności od poślizgu s silnika indukcyjnego

39 Projektowanie muzyn elektrycznych