476 (6)

A7ft 12. PftdY i elektromagnetyczny moment obrotowy maszyny indukcyjnej

A7ft 12. PftdY i elektromagnetyczny moment obrotowy maszyny indukcyjnej

kiL —

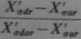
(12.731?)

oznaczenia — jak we wzorach (12.61) oraz (12.68).

W dalszych rozważaniach posłużono się współczynnikami wg zależności (1273). Wówczas zastępcza rezystancja

oraz reaktancja

R'ir ~ R*r( 1 ~^dt) +R^orktu

X'dr — 2f«ar(l ~ ku) + X'_aiork_tL

(12.74a)

(12.75a)

przy czym po przekształceniach otrzymuje się współczynniki

kji —

(l+u^+K^) bIBS

(l₊^fe)W

(I +o_xa,²)(l +<g^a+a^a^~^j a_x(I +aj(l +a_r)² (1 +a_xa,²)(l +*,)²+s²(—J(1 +u_xo_r²)(l +aj²

(1274b)

(1275b)

w których: a_x — wg (12.67a); a_r — wg (12.69); pozostałe oznaczenia — jak na rys. 127.

Pomijając bardzo mały składnik a_xa? < 1, otrzymuje się

(12.74c)

(12.75c)

I BBBib

(1 +a,)²+s² 0g^J(l +flj² (l+a,)²+s²f—^(l+aJO+a,)²

kdL *    i    / V" Cl

(l+fl,)²+^(-^J (1+aJ²

Wzory (1274) i (12.75) można jeszcze bardziej uprościć przystosowując je do poszczególnych struktur uzwojeń klatkowych. Na przykład w obliczeniach uzwojenia z prętami umieszczonymi we wspólnych żłobkach, w którym X'„_t * 0, współczynnik

12.7. Obliczania silnika o wirniku dwuklatkowym

477

k_dm «

(12.76a)

natomiast współczynnik

(1+a,)²

(12.76b)

(1+a,

W projektowaniu silnika dąży się do tego, żeby stosunek X'„₂/Rri * 1 oraz żeby R',2 < R’_rl i X’„, < X'„₂, wówczas uzyskuje się bowiem duży wskaźnik dobroci rozruchu. Dlatego w obliczeniach projektowych wymiarów uzwojeń klatkowych dla zadanych wymagań rozruchowych, tj. dla poślizgu «»1, można posługiwać się zależnościami

(I277a)

(12.77b)

_ (l+a^+s^l+aj (1 +a,)²a_r+s²a_r

"■~(l+a_r)²+s²

Dokładne obliczenia maksymalnego elektromagnetycznego momentu obrotowego M,*, poślizgu krytycznego s_b oraz przedążalności momentem m_b silnika dwuklatkowego są znacznie bardzie) złożone niż opisane w p. 12.5. Jeżeli bowiem rezystancję oraz reaktancję zastępczą wirnika wg wzorów (12.61) podstawi się do zależności (1232a) albo jeżeli skorygowane parametry wirnika podstawi się do zależności (12.32b), to otrzyma się bardzo skomplikowaną funkcję M_m(s). W celu analitycznego wyrażenia poślizgu krytycznego należałoby pochodną tej funkcji względem poślizgu przyrównać do zera. Otrzymuje się wówczas równanie piątego stopnia względem poślizgu i jego analityczne rozwiązanie nie jest możliwe. Tym bardziej nie można analitycznie wyrazić elektromagnetycznego momentu obrotowego krytycznego M,„ w zależności od rezystancji i reak Uncji uzwojeń. Wartość momentu krytycznego można wyznaczyć na podstawie wykresów kołowych maszyny o wirniku dwuklatkowym [12.2; 12.3].

W projektowaniu wspomaganym komputerem moment obrotowy krytyczny oraz przeciążalnośd momentem można obliczyć za pomocą algorytmu metodą kolejnych przybliżeń. Na przykład w pierwszym przybliżeniu — tj. w pierwszej iteracji wartość poślizgu krytycznego oblicza się wg wzorów (12.37), przyjmując parametry uzwojenia wirnika w stanie jałowym wg zależności (12.68). Dla tak otrzymanego poślizgu s_M oblicza się parametry wirnika wg wzoru (12.61) i ponownie wyznacza wartość poślizgu s»j, a następnie — wg wzoru (12.32a) — oblicza moment elektromagnetyczny obrotowy. Nadając