zadania z matmy012 bmp

y'—2y — t
jednorodne v'-2 v = O y=2 y
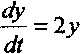

In v = 2t + InC y m Ce2'
y=y%,+y^
= Ąt + Ą
JW = 4
Ą —2 (Jt# +J0) = # -24f + (4-2J0) = -24 =1 yi, 2 — O
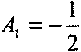
-|-2Ą=0
£*
Wyszukiwarka
Podobne podstrony:
zadania z matmy013 bmp y ~2y = 2# jednorodne y’~2y - O y =2y {!} - 2 v dl ^ = 2 dl y In _v = 2t
zadania z matmy014 bmp v-v~smi /-2j = 2siiil jednorodne f~2y = 2y = 2 dl dydtdy y In v = 2/ + In C y
zadania z matmy006 bmp 4 /fcj)=/Q (równanie o postaci jednorodnej y_£±Z = 0H.,=2t + y -t+y = t t i t
zadania z matmy011 bmp II. (y ~2ty^t i> U=0 jednorodne y -2ty = O dy dty In r -r i InCy = &
zadania z matmy015 bmp jednorodne y -ytgx = Oy =ytf& dy—~ = ytgx dx dy - tgxdx ł c y In v
zadania z matmy018 bmp ł-r jednorodne
zadania z matmy001 bmp dy = sin" xdx fdy = [sin2 -urtc + C 1 1 y -.....x-----
zadania z matmy004 bmp 3. f(x, v) “ f(ax ł by + c b ?- O(riw«»«If o postaci /(«+%+c) /=-sj2x+3y-l ax
zadania z matmy007 bmp y +x XV - 7 f „V y x f y i 1 — 1 y2 +x2 _ 2 2 X X
zadania z matmy008 bmp Hxty) (równanie postaci różniczkowej Ąx,y)dx+Q(x,y)dy = 0) e
zadania z matmy009 bmp Q(x,y) = SF(x,y)/8y(3) ^ &CM). ^ Z (2):F(x,y) = f P(x,y) dx= f (ex simy +
zadania z matmy016 bmp III. Określić rozwiązania równań Bernoulliego y +p(x)y ~ q(x)yA lub odpowiedn
zadania z matmy017 bmp = —sin/yŁ 1 V* y — m-z— + •, = ~sm/ 2 j2 y ! fłt ( -tY —-
MATEMATYKA. n In 2’T . Podaj cosx+sin>d f 3n 36. Narysuj wykres funkcji: f(x) =
poprawa z rozniczek2 Zadanie 3. (5p) Wyznaczyć ekstrema funkcji /(x, y) — y In (y + 2x2). Si: z = 12
1. Rozwiązać układ równań liniowych 2 1 5 3 {x + 2y — z + 3t + w 4x — y + z — 2t + w 6x + 3y —
47313 Scan Pic0042 Zadanie 3.15 Przenosząc ładunek 1 C w jednorodnym polu elektrycznym na odległość
więcej podobnych podstron