skan0151

154 Roztwory i równowagi fazowe

zJ/fjn, jest graniczną wartością całkowitego ciepła rozpuszczania:

AH?_m = lim

ⁿ2 ^: n i —> 0

Ze schematu 4.2 wynika oczywisty związek między tymi efektami:

0_r = A HZ - AH_ml.

Przykład 4.12. W tabeli poniżej zestawiono wyniki^ pomiarów całkowitego ciepła rozpuszczania 1 mola HN0₃ w n_x molach wody w 25°C [kJ ■ mol^-1]

"1	1	2	3	4	5	6	8	10	15
477jnt	-13,11	-20,08	-24,3	-26,98	-28,73	-29,84	-31,12	-31,84	-32,46
«1	20	30	40	50	75	100	200	500	1000
4//int	-32,67	-32,76	-32,75	-32,74	-32,74	-32,75	-32,8	-32,9	-32,98

Podczas rozpuszczania jednego mola kwasu w nieskończenie dużej ilości wody w tej temperaturze zostaje wydzielone 33,34 kJ • mol^-1.

a)    wykreślić zależność AH_m{^m) i &_T(y!m) oraz molowej entalpii mieszania H™(x₂), a także znaleźć ich równania. Wyznaczyć na tej podstawie cząstkowe molowe entalpie mieszania w roztworze zawierającym 4 mole wody na 1 mol kwasu.

b)    Obliczyć zmianę entalpii po dodaniu, w 25°C, 1000 g wody do roztworu A, zawierającego 1748,9 g HN0₃ rozpuszczonych w 1000 g H₂0 (n_{ : n₂ = 2 : 1).

c)    Pojemność cieplna w 25°C wodnego roztworu HN0₃ o ułamku molowym x₂ = 0,25 wynosi 2,78 J ■ K^-1 • g^-1. O ile wzrośnie temperatura naczynia zawierającego 400 g w^rody (o temperaturze początkowej 25°C), gdy szybko wprowadzi się do niej taką ilość HN0₃, by ułamek molowy kwasu wyniósł 0,25?

Rozwiązanie, a) Przekształcając nieznacznie w'zór (4.4) dla M_] = 18,015 [g • mol^-1], obliczamy molalność [mol • kg^-1] poszczególnych roztworów, wstawiając za n₂ 1 mol:

1000 n_lM_l '

Ułamek molowy kwasu dla n₂ = 1 mol obliczamy zc wzoru (4.2):

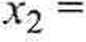
_1_

?7( + 1

K.P. Miszczenko, A.A. Rawdiel, Zbiór wielkości fizykochemicznych, PWN, Warszawa 1974, s. 56.