File0039 (2)

2) dla 3C * X^    ^    - sprzężenia krytyczne, mamy również

jeden punkt ekstremalny 1

U

o |x»0

3) dla X> ^ mamy trzy punkty ekstremalne dla = 0    1

-5    - ten stan nazywamy sprzężeniem

0.    nadkry tycznym.

U₂

• 11 V?⁷

Wykres krzywych rezonansowych g- dla trzech różnych przypadków ,    o

sprzężeń przedstawia rys.24.8.

Na uwagę zasługuję następujące faktys

1)    częstość średnia Jest funkcję wielkości sprzężenia, czyli parametru X (wzór (24.44)) i tylko na wykresie krzywych rezonansowych w funkcji częstości względnej x otrzymane wykresy dla różnych maję maksimum dla tej samej wartości x ■ 0;

2)    w przypadku braku sprzężenia x « 0, do drugiego obwodu rs -zonansowego energia nie Jest przekazywana, więc nie wykonuje drgań

Aby

Natomiast pierwszy układ drga z częstościę -.ł___

to pokazać zauważmy, że ze wzoru (24.46) mamy V^~C

A

tu

bo

1 + 8 <ł² x² ♦ 16 x⁴ Q⁴

-j ♦ (2 x)²

Ca) - tO

śr

co

H-0

Pręd X₃ obliczymy znajęc A podobnie Jak obliczaliśmy A

- { - *( C+J łj² L C) - j^coR C*j(co² L C-1)]}(-U₀«C)

co² r² c + (o² u c - i)² u uc ;

O

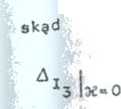
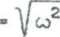
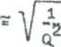
-n * (?- x)² U WC

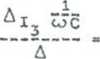
1

Oest to wzór Identyczny jak otrzymany poprzednio;

3) dla zastosowań filtracyjnych największe znaczenie ma sprzę -Zonie krytyczne 3€ - 3? ^ lub nadkrytyczne at > ae Parametrem możemy kształtować charakterystykę filtracyjną i pomimo że tracimy maksymalny współczynnik uwielokrotnienia amplitudy, który jest równy g (w układzie niesprzężony® 0.), jak i zwiększa się nachylenie charakterystyki na krawędziach pasma, bo

_i 2

f (x)i    ,    » +    - układ niesprzężony

'* * ♦ aa ^

2

f"(x).    .    ■ ♦ ~ - układ sprzężony krytycznie

x * +----- ²

' V?Q

zyskujemy na tym, Ze w pobliżu rezonansu charakterystyka w układzie sprzężonym jest bardziej płaska niż w układzie nie-sprzężonym.

24.2, Opis układu pomiarowego

Układ pomiarowy składa się z:

-    generatora napięcia sinusoidalnego o przestrojonej częstotliwości - dekadowe ustawienie częstotliwości, przy czym od -czyt należy mnożyć przez wartość w okienku mnożnika;

-    woltomierza z sondę;

-    pudełka z obwodami rezonansowymi z dołączonymi do niego trzema kondensatorami wymiennymi do wtyków C_g.

73