img298 (7)

J elementy kolumn j zmiennych decyzyjnych

Obecnie wszystkie zmienne niebazowe mają dodatnie kryterium simpleks, a więc wartości funkcji celu nie da się już zmniejszyć.

Pozostawiając Czytelnikowi obliczenie elementów tablic pośrednich, poniżej (posługując się rachunkiem macierzowym) obliczono poszczególne elementy tablicy końcowej¹.

clB 'A = [1000 2400]

1 0

0 1

1,5

-0,5

= [1000 2400 300]

yi> y₂ i y₃>

y i y 2

~y 7	, więc B =	2	3	, B '= i	'3 -31 .-1 2_|~	' 1 -f 1 2	<- i
		1	3	3
		L J				71 1-

elementy kolumn zmiennych sztucznych , ^S1 ' ^2’

?-i

B~^xb =

	1	-1	[2 3	1,5"		"l
	1	2	1 3	0		0
	L 3	3 J
	' 1	-1"	[301		"10 '
^=	1	2	20	—	10
	. 3	3 J			L3

wartości zmiennych bazowych (rozwiązanie),

i- o o o o 0 1 _	, więc clB~^1 = [1000 2400]	' 1 1	-f 2	= [200 600] <-	elementy wiersza Zj dla kolumn
		71	T.		ii i s2,

elementy wiersza z_;-dla kolumn

c£B~¹b = [1000 2400]

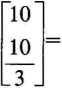
10000 + 8000 = 18 000

wartość funkcji celu.

Optymalne rozwiązanie programu dualnego jest zatem następujące:

/i = 10,    /₂= y,    F[y\,y\)= 18000.

Zauważmy jeszcze, że z ostatniej tablicy simpleksowej można odczytać także rozwiązanie optymalne programu dualnego. Mianowicie, optymalne wartości zmiennych decyzyjnych PD są równe wartościom bezwzględnym

liczb występujących w wierszu zerowym    ostatniej tablicy simpleksowej,

odpowiadających zmiennym swobodnym PP (por. tabl. 42): y\ =| — 10| = 10,

10

T’

l'2 =

^3 = 0. Analogicznie, wartości zmiennych decyzyjnych PP są

równe wartościom bezwzględnym liczb występujących w wierszu zerowym ostatniej tablicy simpleksowej PD, odpowiadających zmiennym swobodnym lego programu (por. tabl. 46: xj = |200| = 200, x\ = |600| = 600).

Pytania i problemy

1.    Dany jest program liniowy:

*!+ x₂+x₃ = 30, x_i+2x₂+x₃'^l0,

2x₂ + x₃ ^ 20, x₂, x₂, x₃^0,

2x_y + x₂ + 3jc₃-* max.

Sprowadzić powyższy program do postaci kanonicznej.

2.    W powyższym PL wektor optymalnych zmiennych bazowych jest następujący:

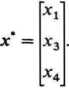
Podać rozwiązanie optymalne i wartość funkcji celu dla rozwiązania optymalnego.

3.    Co to jest „wiersz zerowy” tablicy simpleksowej?

4.    Omówić sposób zmiany bazy w kolejnych iteracjach algorytmu simpleks.

5.    Który z poniższych wektorów (gdzie x₁₍ x₂ i x₃ to zmienne dcyzyjne, x_ir i x_} to zmienne swobodne, a s₃ i s₂ to zmienne sztuczne) nie jest wektorem optymalnym i dlaczego?

				*1
		*1		*3
*3	, X =	*3	X =	*4
i*’		fl
				x2.

1.5. Analiza wrażliwości

Rozwiązanie programu liniowego jest dopiero początkiem analizy problemu. Podejmujący decyzje powinien także wiedzieć, jak wrażliwe jest uzyskane rozwiązanie optymalne na pewne zmiany w założeniach modelu lub zmiany czynników zewnętrznych (parametrów modelu). Odpowiedź na te pytania ułatwia analiza wrażliwości (ang. sensitivity analysis) rozwiązania optymalnego na zmiany niektórych parametrów modelu, a więc na przykład: a) współczynników funkcji celu (OFC - objective function coefficients), najczęściej cen - analiza wrażliwości pozwala w tym przypadku odpowiedzieć na pytanie, w jakich granicach mogą się zmieniać te parametry, aby dotychczasowe rozwiązanie pozostało optymalne;

53

1

Zauważmy, że ponieważ ,v, = —y_Ą, a s₂— —y₅, współczynniki kolumn zmiennych swobodnych są wziętymi ze znakiem przeciwnym współczynikami kolumn odpowiadających im zmiennych sztucznych.