0449

451

5 5. Elementarne funkcje zmiennej zespolonej

Porównując te dwa rozwinięcia widzimy, że

skąd

2c% = — 1,    3c₃ = 1,

= (-I)-¹,

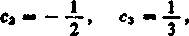
A więc mamy ostatecznie w otoczeniu zera rozwinięcie

(12)

ln(l + w) =    +    ... -f(-l)"-¹ —+ ...

2    3    n

Łatwo sprawdzić, że otrzymany szereg ma promień zbieżności R = 1. Widzieliśmy, że dla dostatecznie małych z jego sumą będzie wartość główna logarytmu ln (1 + w). Czy tak samo będzie w całym kole

M<1?

Ponieważ szereg (12) spełnia formalnie równość

_ew-w¹/2+»¹/3 - ... ₌ 1 _{+ M)j}

przeto spełnia ją też faktycznie dopóki jest zbieżny. A zatem w całym kole |h>1<1 suma szeregu (12) jest na pewno jedną z wartości Ln (l+w). Cale zagadnienie sprowadza się do pytania, czy zawsze będzie to wartość główna.

Jeżeli |m>|<1, a więc punkt przedstawiający liczbę 1 + w leży wewnątrz okręgu o środku w punkcie w = 1 i promieniu równym 1, to arg (1 + w) jest zawarty między — y 7t i -i- 7r, a inne wartości Arg (1+w) są zawarte w przedziałach:

i* -i*)-
(i* !-)•	(ł*ł*)* -

lub

Urojoną składową sumy szeregu (12) jest właśnie Arg(l+M>) [patrz (9)]. Dla dostatecznie małych w — = «+t>/ daje ona wartość główną arg (1+w), tzn. jest zawarta między — y i y tc, a jednocześnie jako funkcja ciągła zmiennych u i u nie może przeskoczyć do innych wspomnianych przedziałów, a więc dla wszystkich | w| < 1 jest ona równa właśnie wartości głównej arg (1 + w). Udowodniliśmy więc, że równość (12) jest spełniona w całym kołe Mci.

Zastępując w (12) w przez — w i odejmując otrzymany w ten sposób szereg od szeregu (12) otrzymujemy pożyteczne rozwinięcie(¹)

(13)

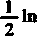
1+w

1—w

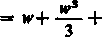
2n—1

+ ...,

które jest zbieżne dla M-Ci.

459. Funkcje trygonometryczne i ich funkcje odwrotne. Wiemy z 404 (12) i (13), że dla x rzeczywistego funkcje cos x i sin x określone są szeregami

O Ponieważ część urojona różnicy ln (1+w)—ln (1 — w) jest zawarta między — it i w, więc różnica

1 + w 1-w*

ta określa właśnie wartość główną ln

29*