0451

453

§ 5. Elementarne funkcje zmiennej zespolonej

Rozwinięcia otrzymane w ustępie 449 dla tg x i funkcji x ctg x zachowują ważność także po podstawieniu zmiennej zespolonej z zamiast rzeczywistej x. Podobieństwo rozwinięć x ctg x i x ctgh x jest całkiem zrozumiałe, jeżeli uwzględnimy otrzymane z (16) zależności

tgyf°=/tghy, ctgyi = — i ctgh y.

Spośród funkcji odwrotnych względem funkcji trygonometrycznych rozpatrzymy tylko arcustangens i arcussinus.

Z uwagi na to, że funkcje trygonometryczne dają się sprowadzić do wykładniczej, należy oczekiwać, że funkcje odwrotne względem nich będą związane z logarytmem.

Zaczniemy od uwagi, że w = tg z nie przyjmuje wartości ±i (łatwo można to wykazać rozumując nie wprost). Niech będzie w=£±i. Równanie

f-e-”    1    e^2,t-l_„

* i e“+e-”    «    e²“+l

można wtedy rozwiązać względem z:

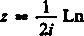
1 + wi 1 — wi

,2.1 ₌ l + w>f 1 -wi ’

Jest to właśnie wzór na funkcję odwrotną Arc tg w, która jest oczywiście nieskończenie wielowartościowa tak samo jak Ln.

Gdv weźmiemy wartość główną logarytmu, otrzymamy wartość główną

aretg w = ln-fi— (w ¥> ±0,

która ma tę własność, że jęj część rzeczywista jest zawarta w przedziale (—

- |it < R (arc tg w) <    .

Pozostałe wartości otrzymujemy ze wzoru

Arc tg w = arc tg w-ffot (k — liczba całkowita).

Zastępując w szeregu (13) w przez wi otrzymamy rozwinięcie dla gałęzi głównej arcusa tangen sa

arc tg w = w— — + ... +(-l)"^_l —--1- ...,

3    2n-l

które jest zbieżne dla |h>| < lf¹).

Przejdźmy teraz do rozwiązania równania

sin z =

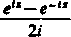
w

względem z:

e²¹’—Iwt-e¹¹— 1 = 0, e^,z = w/± |/l — w^x ,

skąd

z “ Arc sin w = -i- Ln (w/± j/l — w²) . Otrzymujemy tu też funkcję nieskończenie wielowartośdową. ¹

1

Gdy w » ±i, funkcja arc tg w ma wartość nieskończoną.