89124 str116 (5)

116 I. LEMENTY TEORII FUNKCJI ZMIENNEJ ZESPOLONEJ

Zadanie 11.18. Wyznaczyć potencjał (p(x,y) płaskiego pola elektrostatycznego wytworzonego w środowisku nie przewodzącym przez przewodnik ograniczony powierzchnią walcową o równaniu x²+(y—3)² = 5 o stałym potencjale F_o>0. Przewód ten umieszczony jest nad płaszczyzną y — 0 o potencjale równym zero.

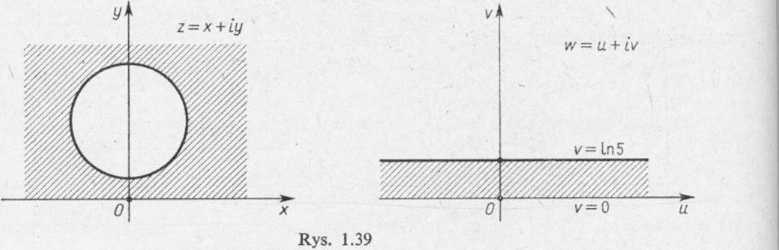
Rozwiązać podane zagadnienie wiedząc, że funkcja

z — 2/

w (z) = u + iv = 2i ln-

z+2i

przekształca obszar płaski zawarty między okręgiem K = x²+(y— 3)²—5 = 0 i prostą y = 0 na pasmo 0<«<ln5 (patrz rys. 1.39).

Rozwiązanie. Po rozdzieleniu części rzeczywistej i części urojonej w funkcji iv(z)

w(z) — u + iv — —2Arg

z—2/ z+ 2/

+ /ln

x²+y²—4y + 4 x² + y² + 4y + 4

możemy zauważyć, że funkcja w>(z) przekształca okrąg x²+(y—3)² — 5 = 0 w prostą v = ln5, natomiast prostą y = 0 w prostą v — 0. Potencjał cp(u,v) odwzorowanego pola elektrostatycznego przez funkcję w(z) w paśmie 0<i’<ln5 spełnia następujące warunki brzegowe:

(p (u, 0) = 0 i (p (u, ln 5) = V₀,

Zadania do rozwiązania

1.    Znaleźć funkcję, która tr Zi = (3 + 2/), z₂ = (7+2/), z₃ ramienny OB^Cj o wierzchołl wierzchołki z_k przechodzą odp

2.    Znaleźć przekształcenie 1 wistą, aby punktom —i, 1, i <

3.    Znaleźć odwzorowanie kc przeprowadzające punkty oo, (

4.    Znaleźć funkcję w = /( w siebie i taką, aby:

a)    /(i) = 0, Arg/'(i) = *it

b)    /(O) = 0, Arg/'(0) = -1

5.    Znaleźć funkcję w = f(z w koło jednostkowe i taką, ał

6.    Na jaki obszar w plaszc: |z|<l?

7.    Znaleźć funkcję, która c wzdłuż odcinka łączącego pui

8.    Znaleźć funkcję, która od odcinka <0, id) w górną półp

9.    Z górnej półpłaszczyzny (rys. 1.40). Znaleźć funkcję, któ wany na rys. 1.40) na górną ]

zatem <p(u, v) jest funkcją o następującej postaci:

ln 5

Jeżeli do powyższej zależności na miejsce zmiennej v podstawimy część urojoną funkcji w(z), to otrzymamy funkcję <p(x, y) określającą rozkład potencjału w rozważanym polu elektrostatycznym. Jest to następującą funkcja:

<P(x,y) =

V₀ x² + y²+4y+4

— ln —=-r-.

ln 5 x +y — 4y+4

10. Znaleźć funkcję, która c półpłaszczyznę.