Elektronikawzad63

W. Cnżymki HLIiKTRONTKA W ZADANIACH

Ot*ć 2 A mli za wpływu rmian temperatury n» prKt układów półprzewodnikowych

£/- =L'„+«;■/, =£/„ +-^—(f/_M-3t/„)    (2.12.2)

i\| T A2

Rezystory /?/ i musimy dobrać w sposób zapewniający kompensację zmian temperaturowych napięcia odniesienia. Do zależności (2.12.2) powrócimy po dokonaniu tego wyboru. Teraz zwróćmy tylko uwagę, źe napięcie odniesienia nie zależy od prądu polaryzacji 1. Prąd / musi być tylko wystarczająco duży, aby mógł popłynąć wynikający z prądu emitera (zależnego od wybranych Ri i R₂) prąd bazy l_B = Ie/0+1), a reszta płynąca przez diodę stabilizacyjną mogła zapewnić odpowiedni punkt pracy na jej charakterystyce w zakresie przebicia. Warunek / > If./(f$* 1) zostanie uwzględniony przy wyborze rezystorów R) i R₂.

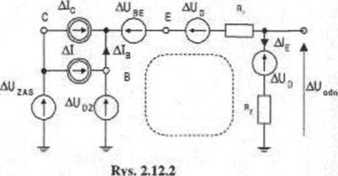
Rozwiązanie zilustrujemy za pomocą schematu zastępczego układu dla zmian temperatury przedstawionego na rysunku 2.12.2. Schemat zawiera siedem źródeł wymuszających, które dla małych przyrostów temperatury traktujemy jako liniowe. Możemy więc zastosować zasadę superpozycji, czyli obliczyć prąd Ala tranzystora jako sumę składowych pochodzących od tych źródeł (w tym także nieznanego Ale) występujących osobno, oraz jako drugie równanie o niewiadomych Alg i Ale wykorzystać zależność (W2.7), a interesujący nas przyrost prądu AIe wyznaczyć jako sumę AJ e= Al u + Ale.

W naszym przypadku jest to jednak droga niepotrzebnie zbyt skomplikowana. Patrząc bowiem na rys. 2.12.2 możemy zauważyć, że każdy z prądów cząstkowych wynikających z SPM równych Ale i Al (obliczany przy zwartych SEM) krąży w obwodzie o zerowej rezystancji omijając obwód emitera. Z kolei zmiana napięcia zasilającego AUzas jest odcięta od obwodu emitera przez dwie SPM, które analizując wpływ AUzas należałoby rozewrzeć. Przyrost prądu emitera można obliczyć wprost z obwodu oznaczonego linią przerywaną jako:

AL

A(/_D2-3AU,

R_t+R₂

czyli zmiana napięcia odniesienia wynosi:

AU

AU„ +/?, A/r=AU_n+-

Ą + R.

■(AU,_W-3AU₀)

(2.12.3)

(2.12.4)

Równanie lo jest oczywiście różnicowy (przyrostową) postacią równania (2.12.2) i równie dobrze moglibyśmy nie wykorzystując schematu zastępczego otrzymać je różniczkując równanie (2.12.2). Aby AU od* było równe zeru musi zachodzić:

W naszym przypadku:

AU₀(1-

Skąd mamy:

A U,„

AU,

3*2 1-	At/,„		(2.12.5)
R^R.	ff, + R2
	czyli	*i _2 _2 ^£W-	(2.12.6)
		R. A Uu £„

,

Ad 2. Teraz już z równania (2.12.2) można obliczyć wartość napięcia odniesienia:

•(<'„, -3U„)=0,ÓV +

= 1,95 V (2.12.8)

=(/„+-

6,2 V-3 0,6 V

R_t/R₂ + \    2,26+1

czyli spadek napięcia na rezystancji R₂ wynikający z przepływu prądu If, wynosi 1,95 V - 0,6 V = 1,35 V. Maksymalny prąd emitera wynosi /£=/?•/ =100 • 0,1 mA = 10,1 mA. Przyjmując na przykład prąd równy połowie maksymalnej wartości, tzn. Ir. - 5 mA (wtedy połowa prądu / przepływa przez diodę stabilizacyjną) otrzymujemy:

R₂ = 1,35 V/5mA = 270Cl, oraz R, = 2,26 • R₂ = 2.26 • 270 Cl = 610 O

Ad 3. Zwróćmy w tym miejscu uwagę, że przez emiter nie płyną składowe prądu pochodzące od Ale i Al tylko dzięki zerowej rezystancji dynamicznej diody stabilizacyjnej raz. W przypadku konieczności uwzględnienia tej rezystancji zarówno Air jak i Al rozpływają się na dwie równoległe gałęzie o rezystancjach odpowiednio równych Rt + R₂ i raz. Wtedy przyrost prądu emitera Air (a więc i przyrost napięcia odniesienia) zależy także od Alę i AI_y a więc musimy przejść pełną naszkicowaną powyżej drogę obliczeń wykorzystując odpowiednio zmodyfikowany (patrz rysunek 2.12.3) schemat zastępczy dla zmian temperatury.

Konieczność uwzględnienia rezystancji dynamicznych rgr i r_D nic stwarza natomiast większych trudności obliczeniowych, gdyż na schemacie zastępczym z rysunku 2.12.3 okazują się one włączone szeregowo z odpowiednimi rezystorami. Uzyskane w punkcie I i 2 rozwiązanie dla przypadku roz = 0 ma nadal wartość, gdyż można do niego podstawić:

oraz    R₂ = R₂ * + rm    (2.12.9)

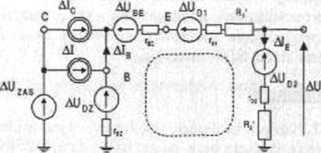
Rys. 2.12.3

A

*i

= 2-

0,6 mV / °C -2,3 mV/°C

= 2 + 0,26 = 2,26

(2.12.7)

/?/ = /?/’ + raF. + fpj czyli w układzie włączyć odpowiednio zmniejszone rezystancje R/' i R₂‘. Przy większych rezystancjach dynamicznych mogłoby okazać się konieczne przyjęcie większych wartości R₂ i R₂ przy zachowaniu ich obliczonego stosunku.

Ad 4. Zmiany temperaturowe

napięcia zasilającego nie mają w układzie żadnego wpływu na uzyskiwane wyniki, gdyż SEM równa A Uzas jest od reszty' układu oddzielona dwoma SPM (które przy obliczaniu wpływu AUzas należy wyłączyć, tzn. rozewrzeć). Wpływ ten (oraz ewentualnie wpływ rezystancji wyjściowej tego źródła) mógłby się ujawnić przy uwzględnieniu skończonej rezystancji wewnętrznej źródła prądowego AJ (czyli po rezygnacji z założenia, że jest to źródło idealne) i / lub Ale (czyli po uwzględnieniu rzeczywistego nachylenia charakterystyk wyjściowych tranzystora).