56217 prigogine14

Dylemat Epikura

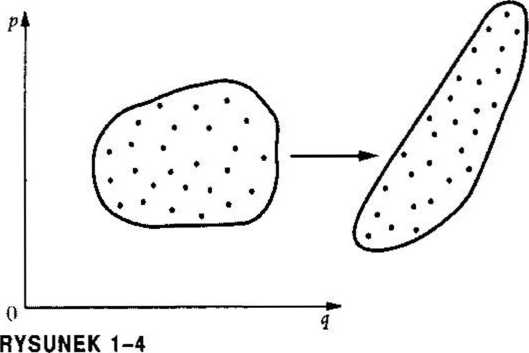
Zespół Gibbsa przedstawiony w postaci obłoku punktów, odpowiadających różnym warunkom początkowym.

własności funkcji delta wrócimy jeszcze w dalszej części książki. Na razie podkreślmy tylko, że należą one do klasy funkcji uogólnionych, czyli dystrybucji (nie mylić z rozkładami prawdopodobieństwa). Istotnie bowiem, ponieważ przy jc = x₀, funkcja - x₀) staje się rozbieżna, to znaczy dąży do nieskończoności, dystrybucje posiadają właściwości zupełnie odmienne niż funkcje zwykłe. Zaznaczmy przy tym od razu, że można je stosować tylko w połączeniu z funkcjami zwykłymi, jakimi są funkcje próbne cp(x). Konieczność wprowadzenia funkcji próbnej odegra kluczową rolę w proponowanym przeze mnie uogólnieniu dynamiki. Na razie jednak zwrócę tylko uwagę na to, że mamy tu do czynienia z odwróceniem perspektywy:.podczas gdy opis układu indywidualnego intuicyjnie wydaje się być sytuacją pierwotną, w przypadku rozpatrywania zespołów staje się on sytuacją szczególną, implikującą wprowadzenie funkcji 5 o specyficznych właściwościach.

Dla Gibbsa i Einsteina teoria zespołów była jedynie praktycznym narzędziem przeprowadzania obliczeń przy braku znajomości warunków początkowych. Z tego punktu widzenia prawdopodobieństwa rzeczywiście są wyrazem naszej niewiedzy, braku informacji. Było dla nich rzeczą oczywistą, że w dynamice badanie pojedynczych trajektorii i analiza rozkładów prawdopodobieństwa to jedno i to samo. Wychodząc od indywidualnych trajektorii, można otrzymać ewolucję funkcji prawdopodobieństwa, i na odwrót. Prawdopodobieństwo jest po prostu jednoznaczne z superpozycją trajektorii i nie prowadzi do żadnej nowej właściwości. Obydwa poziomy opisu, poziom indywidualny (odpowiadający pojedynczym trajektoriom) oraz poziom statystyczny (odpowiadający prawdopodobieństwom) są w takim wypadku równoważne.

Ale czy tak jest zawsze? Jeśli chodzi o układy stabilne, gdzie problem nieodwracalności w ogóle nie istnieje, Gibbs i Einstein mieli rację: indywidualny punkt widzenia jest równoważny z ujęciem statystycznym. Można to bardzo łatwo sprawdzić i powrócimy jeszcze do tego tematu w rozdziale 5. Co jednak dzieje się w przypadku układów niestabilnych? Dlaczego wszystkie teorie, dotyczące procesów nieodwracalnych, jak chociażby kinetyczna teoria Boltz-manna, badają prawdopodobieństwa, a nie trajektorie? Czy jedynym tego powodem jest stosowanie przybliżeń i gruboziarnisty charakter naszych opisów? Jak zatem wytłumaczyć wielki sukces teorii kinetycznej, jej eksperymentalnie zweryfikowane iloś-

47