67678 new 53 (2)

108

6. Obliczenia gwintów

W celu określenia wytrzymałości złożonej (zginanie i ścinanie) półeczkę gwintu można potraktować jak belkę wspornikową o wysięgu

szerokości b = ndin (długość obciążonej nitki gwintu) i grubości g

(patrz rys. 6.18). Naprężenia zginające gwintu śruby (w nakrętce są one mniejsze, ponieważ większa jest szerokość półki gwintu) wyrażają się wzorem

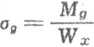
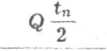
rc d, ng*

3 Q t_n^Kd)ng² '

(6.49)

Naprężenia ścinające w tym samym przekroju są równe

(6.50)

Q_

r.d_tng

Warunkiem wytrzymałości zgodnie z hipotezą Kubera jest aby naprężenia zastępcze o_z nie przekraczały wartości naprężeń dopuszczalnych na zginanie k_g, czyli

», = iĄ + 3r’ - -jiL- /3 < k, (6.5D

W gwintach metrycznych (tabl. 2.1) istnieją następujące zależności: tn = |-H, H = y P, g = jP, ^ 0,7, stąd

Oz — 2,77- <k_g. (6.52)

Na podstawie zależności (6.48) i (6.52) otrzymamy

<0,5

d,

d_s

kg.

(6.53)

6.3. Obliczenia wytrzymałościowe gwintu

109

Aby spełniony był warunek wytrzymałości złożonej według (6.51) dla gwintów metrycznych wystarczy, aby naciski na powierzchni gwintu nie przekroczyły wartości określonych równaniem (6.53). Dla gwintów trapezowych symetrycznych, trapezowych niesymetrycznych i gwintów prostokątnych (przy t_n = g) stosunek głębokości nośnej gwintu do grubości — wynosi odpowiednio 0,7886, 1,0188 i 1, a stąd współczynnik licz-2

bowy we wzorze (6.53) jest odpowiednio równy 0,43, 0,28 i 0,29. Wynika stąd, że dla spełnienia warunku wytrzymałości złożonej naciski na powierzchniach tych gwintów powinny być znacznie mniejsze niż w gwintach trójkątnych.

Z porównania gwintów o różnych zarysach i identycznej głębokości i długości skręcenia (rys. 6.19) również wynika, że gwinty trójkątne mają największą wytrzymałość, gdyż ich grubość g jest największa. Z powodów wyżej wymienionych a także ze względu na dużą samohamowność gwinty trójkątne stosowane są we wszelkiego rodzaju połączeniach złącz-nych.

Rys. 6.19. Porównanie gwintów o różnych zarysach

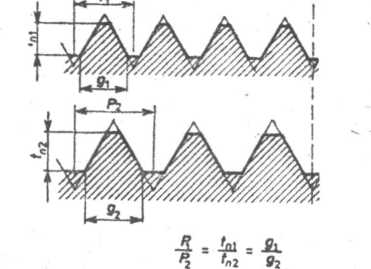
Rys. 6.20. Porównanie gwintów o różnych podziałkach