62596 MATEMATYKA145

280 V Całka oznaczona

4. ZASTOSOWANIA GEOMETRYCZNE CAŁKI OZNACZONEJ

DŁUGOŚĆ ŁUKU. Na początku zajmiemy się przypadkiem, gdy luk / dany jest równaniem jawnym y - f(x), a£x£b, gdzie f jest funkcją ciągłą na przedziale <a,b >. Najpierw określimy długość |/| tego luku Określenie to będzie zgodne z intuicyjnym rozumieniem długości i da nani sposób obliczenia tej długości

Nicchzatcm a=x₀ <x, <...<x_n_, <x_n=b oraz Ax, x,-x, , 5_n = max{Ax^.., Ax_n}, A, = (x_|tf(x_i)), i = l,2,...,n, Punkty A, dzielą luk /- AB na luki częściowe AyA,,..., A_n ,A_n, (por. rys 4.1).

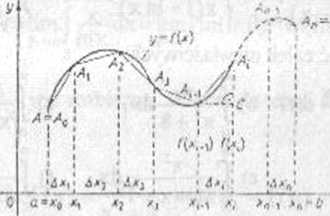
Rys 4 I

Niech l_n oznacza łamaną o wierzchołkach A₀, A,,...,A_n, |/J - długość tej łamanej

l^/nH^AAM^AiA_Jl+...+|A_B ,AJ,

a d_n- długość największego z jej boków, czyli

d_n - max{|A₀A_l|,...|A_n_,AJ}.

Długość łamanej l_n jest przybliżoną wartością długości łuku /: |/_n|*|/|.

Utwórzmy teraz normalny ciąg podziałów przedziału <a,b > na przedziały częściowe (oznacza to, żc 5„ -> 0, gdy n —> co) i weźmy pod uwagę odpowiadający mu ciąg łamanych (/_n) oraz ciąg ich długości

Jeżeli dla każdego normalnego ciągu podziałów przedziału < a,b >, odpowiadający mu ciąg (|/J) długości łamanych jest zbieżny do tej samej granicy, to tę granicę nazywamy długością |/| luku /. Zatem

dif    i*

(4.1)    |/| = lim |/J= lim £|A, ,A,|.

n *•*    n-»>o

(d„-»0)    ^,el

Pozostaje obliczyć tę granicę. Uczynimy to w dowodzie następującego twierdzenia.

TWIERDZENIE 4.1 Jeżeli łuk / jest wykresem funkcji y - f(x) klasy C¹ na przedziale < a, b >, to jego długość |/| wyraża się wzorem;

(4.2)    |/|=jVl + [f'(x)Fdx.

*

Dowód. Należy obliczyć granicę (4.1). Obliczymy najpierw długość i-tego boku łamanej. Z trójkąta prostokątnego o wierzchołkach A, ,, C, A, na rysunku 4.1, mamy:

IA, ,A| — V(Ax,)²+[f(x,)-f(x, ,)f.

Zgodnie z twierdzeniem lagrange’a (założenia są spełnione, bo funkcja f jest różniczkowalna na przedziale < x, pK, >)

i)“f'(\)Ax_it gdzie x,.,<x_i<x_it i - 1,2.....n,

więc    __

(I)    |A, ,A,|= ^(Ax,)¹+[f'(x,)Ax₁]^: - V^l+[f'(>f,)]^JAx,

Długość łamanej /„ wyraża się więc wzorem

(2> i/j^ŻV^^(>oFax,

Stąd