222 (34)

444

16. Funkcje charakteryzujące obwody elektryczne

amplitudowo-fazowej oznacza się strzałką zwrot odpowiadający wzrostowi pulsacji o. Przykład charakterystyki amplitudowo-fazowej podany jest na rys. 16.21.

Funkcja T(s) zmiennej zespolonej s odwzorowuje płaszczyznę zmiennej zespolonej s na płaszczyznę zmiennej zespolonej T(s). Ponieważ w punktach osi urojonej na płaszczyźnie zmiennej zespolonej mamy s = jaj, więc całkowita charakterystyka amplitudowo-fazowa jest odwzorowaniem osi urojonej z płaszczyzny zmiennej zespolonej s za pomocą funkcji T{s).

Przykład 1. Rozpatrzymy układ o transmitancji przy założeniu, że k > 0 oraz r > 0. Transmitancja widmowa układu przybiera postać

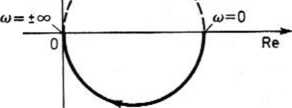
Przy zastosowaniu teorii wykresu kołowego (por. p. 4.9) łatwo wykazać, że charakterystyka amp-litucłowo-fazowa omawianego układu jest okręgiem przedstawionym na rys. 16.22„przy czym wartościom to > 0 odpowiada dolny półokrąg, a wartościom to < 0 — górny półokrąg.

Im

&i<0

\

\

/

\

<Ł/>0

1F

W

0,1 F

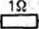
Rys. 16.23. Przykład dwójnika

Rys. 16.22. Charakterystyka amplitudowo-fazO-wa układu z przykładu 1

Przykład 2. Wyz.naczymy charakterystykę amplitudowo-fazową impedancji dwójnika z rys. 16.23. Impedancja operatorowa tego dwójnika wynosi

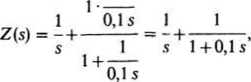
wobec tego transmitancja widmowa

T(jcu) = —+

1    1    .1    1 —j 0,1 (o

jo;⁺1+j 0,1 to ^co 1+0,01 to²’

a stąd części rzeczywista i urojona transmitancji widmowej wyrażają się wzorami:

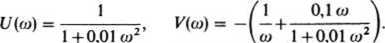
,_V'_Vriik) obliczeń wykonanych na podstawie tych wzorów są następujące:

o), rad/s	U(io), fi	V(o), fi
0	1	— 00
0,1	1	-10,01
0,2	1	- 5,02
0,5	0,997	- 2,05
1	0,990	- 1,10
2	0,962	- 0,69
5	0,800	- 0,60
10	0,500	- 0,60
20	0,200	- 0,45
30	0,100	- 0,33
50	0,038	- 0,21
100	0,010	- 0,11

Charakterystykę amplitudowo-fazową narysowaną na podstawie tych wartości przedstawiono na

_rys. 16.24.

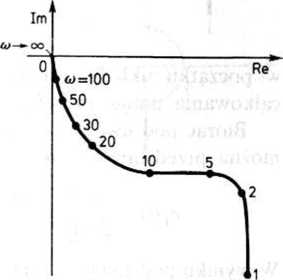
Rys. 16.24. Charakterystyka amplitudowo-fazowa układu z przykładu 2

16.11. Wzory całkowe dla odpowiedzi jednostkowej i impulsowej 16.11.1. Odpowiedź jednostkowa

Wyznaczymy wzór całkowy dla odpowiedzi jednostkowej układu liniowego o transmitancji T(s). Biorąc pod uwagę, że T(s)/s jest transformatą odpowiedzi jednostkowej układu, możemy odpowiedź jednostkową przedstawić w postaci wzoru

(12.2):

(16.101)

16.10. Charakterystyki częstotliwościowe

445

. f T(s)l 1 ^a+r^imT(s)