227 (22)

454

16. Funkcje charakteryzujące obwody elektryczne

a po wykonaniu podobnych przekształceń jak w p. 16.12.2, otrzymujemy

. 2A ^ a>F(cu)cosa)f ,    ,    ,

r_c(t) = f-j-2—dtu + AU (w₀) cos co₀1.    (16.127)

tt o (Oq CO

Całkę w tym wyrażeniu należy traktować w sensie wartości głównej, ze względu na nieograniczoność funkcji podcałkowej w punkcie co = co₀.

Podstawiając ( = 0 do równania (16.127), znajdujemy

U(co₀)=T(oo)--}-^^dco,    (16.128)

n^J0co²-co6

bowiem r_c(0 ⁺ ) = AT(co), co łatwo sprawdzić na podstawie twierdzenia granicznego z p. 12.2. Zależności (16.122) i (16.128) noszą nazwę wzorów Kroniga-Kramersa. W prosty sposób można wykazać, że odpowiedź ustalona układu na wymuszenie

A cos co₀1 ma postać

r,_u(f) = Re[4T(joj₀)e^j''^M],

przy czym /JT(joj₀)e^jtu°' jest odpowiedzią ustaloną układu na wymuszenie /4e^j<“⁰',

wobec tego

r_t._M(t) = /4[l/(cu₀)coscu₀f—K(co₀)sinaj₀t].    (16.129)

Odpowiedź przejściowa układu na wymuszenie A cos co₀t wynosi

2/4 * coV(co) cos cot

r_cp(t) = r_c(t) — r_cu(t) =--J-₂-₂—dcu + A V(a>₀) sin co₀t,

Tl q CO o CO

skąd po podstawieniu wzoru (16.124), otrzymuje się

(16.130)

2/4 * [co₀ F(co₀)—coK(co)] coscot

fcp(t) ⁼ j    2    2    dcO,

Jt o    ca^-co¹

przy czym funkcja podcałkowa jest ciągła w punkcie co = co₀, jeżeli funkcja K(co) jest różniczkowalna.

Wyrażenie (16.130) pozwala obliczyć odpowiedź przejściową układu na wymuszenie /4cosco₀f, gdy znana jest część urojona transmitancji widmowej. Odpowiedź ustaloną układu można obliczyć za pomocą wzoru (16.129). Odpowiedź układu można natomiast otrzymać jako sumę odpowiedzi ustalonej i przejściowej.

Za pomocą wyprowadzonych w p. 16.12.2 i 16.12.3 wzorów można również obliczyć odpowiedź układu na wymuszenie A sin(co₀ r + cp). Wykorzystując wyrażenie

sin(co₀ t + cp) = cos cp sin co₀t + sin cp cos co₀t,

widzimy (zgodnie z zasadą superpozycji), że odpowiedzią układu na wymuszenie A sin(a)₀ t + cp) jest r_v(r) cos cp + r_c(t) sin cp.

Otrzymane wzory całkowe umożliwiają obliczanie za pomocą metod numerycznych odpowiedzi złożonych układów przy wymuszeniu sinusoidalnym .

17. UKŁADY WIELOZACISKOWE

17.1. Wstęp

Przedmiotem rozważań w tym rozdziale będą układy wielozaciskowe o N zaciskach. Najprostszymi przykładami takich układów są dwójniki (N = 2) oraz czwór-niki (jV = 4), które były omawiane poprzednio. Obecnie omówimy ogólne własności układów wielozaciskowych.

Dowolny układ o N zaciskach nazywamy wielobiegunnikiem. Wielobiegunnik mający n wejść nazywamy n-wrotnikiem. Zgodnie z tym określeniem, czwórnik można nazwać dwuwrotnikiem.

Wielobiegunniki o parzystej liczbie zacisków mogą tworzyć dwa rodzaje połączeń mających różną liczbę wejść, jak to ilustruje rys. 17.1. dotyczący układu o .V = 6

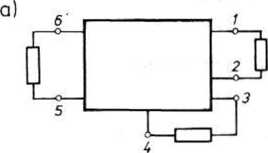
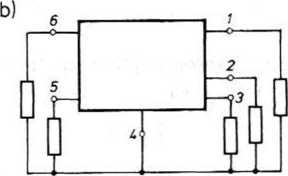
Rys. 17.1. Przykład 3-wrotnika (a) i 5-wrotnika (b) otrzymanego z wielobicgunnika o 6 zaciskach zaciskach. Układ z rys. 17.la ma 3 wejścia, spełniające wuirunek, że prądy w każdej parze zacisków są jednakowe. Układ z rys. 17.Ib ma jeden zacisk wspólny, nazywany również zaciskiem uziemionym: z tego powodu układy tego typu są nazywane m-wrotnikami z zaciskiem wspólnym lub uziemionym, przy czym m = N — \.

Wielobiegunniki o nieparzystej liczbie zacisków mogą tylko tworzyć połączenia jak na rys. 17.Ib; liczba wejść takiego układu jest o 1 mniejsza od ogólnej liczby zacisków.

Teoria wielobicgunników. podobnie jak teoria czwórników. umożliwia analizę