223 (26)

446 16. Funkcje charakteryzujące obwody elektryczne

przy czym a > 2. jeżeli w półpłaszczyżnie Re> z funkcja T(s) jest holomorficzna. Podany wzór jest słuszny, gdy granica T(x.) — lim T(s) ma wartość skończoną.

Zakładamy, że wszystkie bieguny transmitancji T(s) znajdują się po lewej stronie osi urojonej na płaszczyźnie zmiennej zespolonej. Wobec tego bieguny funkcji T(s)/s znajdują się również po lewej stronie osi urojonej, a jedynym wyjątkiem może być biegun jednokrotny s = 0 znajdujący się w początku układu współrzędnych. W tych warunkach jako drogę całkowania w wyrażeniu (16.101) można przyjąć krzywą złożoną z dwóch odcinków osi urojonej oraz pólokręgu C_u o promieniu (> i środku

Im

©

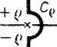
Se

Rys. 16.25. Droga całkowania na płaszczyźnie zmiennej zespolonej

w początku układu współrzędnych (rys. 16.25). Przyjęta w ten sposób krzywa całkowania omija ewentualny biegun s = 0 funkcji T(s)/s.

Biorąc pod uwagę, że w punktach osi urojonej mamy s = jco, zależność (16.101) można przedstawić w postaci

/•,(') =

1

2itj

J

(O

dw+ J

ds+ j

T(}w) ,

e^J"" dco

CO

W wyniku podstawienia Tfjco) = U((o)+}V(m) oraz e^Jt!" = cos euf+j sin cot, otrzymujemy po wykonaniu elementarnych przekształceń

.    1 U (oj) cos cot — Ffcojsinco/ ,

/■jf) = — j--------dco +

2nj

(O

1 V U (oj) cos cot — V(co) sin cot ,

+ — f —-—-d 00 +

:_e

CO

1 J* U (co) sin cot + V(co) cos cot _t

+ — J -dco +

271    O)

1 ^ (co) sin rot + F(co) cos cof    1 _f T(s)

H--I -dco-F——: I -e⁵'ds.

O-rr J    1 m J o

CO

2nj,

Funkcja C/(co) jest parzysta, natomiast funkcja V(a>) jest nieparzysta względem co (por. p. 16.10.1). Łatwo sprawdzić, że suma pierwszych dwóch całek jest równa

_zeru, bowiem funkcje podcałkowe są nieparzyste względem co. Przechodząc do granicy £>-»0, otrzymujemy

.,    1 ⁺,^x t/(co) sin cot + F(co) cos cor ,    1 . 7(s)

r₁(t) = y~ J —^-—-- dco + hm — J    -e^s' ds.

^2jt-x    OJ    _e-0²Kic_o S

Funkcja podcałkowa w pierwszej całce jest parzysta względem co, wobec tego

⁺,^x U (co) sin cot + V{u>) cos (ot ,    . “ U (co) sin cot + F(co) cos cot

1 -dco = 2 I--dco,

o>    o    oj

w związku z tym mamy

1 , 1/(co) sin cot + K(co) cos cot ,    1    7(s)

^ri 0 = -/-^-'-dco + hm — j —— e^ads.    (16.102)

oj    ff-o ^2łtJ c_e 5

Im

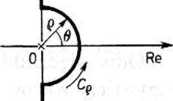
Rys. 16.26. Półokrąg C_fi

W punktach luku C_g mamy s = ge^j® oraz ds = jee^jfld0, przy czym    ę <

^ jak na rys. 16.26, wobec tego

_ - f-e^st ds = — f -tt-jge^jS d0 -*    f dd = - 7(0)

2nj_c^Je s    27rj_^Jn _Q&>° w    2n    2

?^dy 0. Zgodnie z powyższym, równanie (16.102) przybiera postać

.    1 Ł/(co) sin cot + K(co) cos cot 1

r, (t) = - I---dco + - 7(0).

co

(16.103)

•lak

wiadomo, r_t(t) = 0 dla t < 0, wobec tego 1 * 1/(co) sin cot + 7(co) cos cot ,    1

-JJ-<to+j7t0)-0,    <0.