235 (22)

470 18. Schematy blokowe. Grafy sygnałowe Masona

Na podstawie rys. 18.6 otrzymujemy równania:

U₁(s)=U_i(s)+Z_l(s)l(s),    I(s)=-—-,    U₂(s) = Z₂(s)I(s).

R + Z_l{s)+Z₂(s)

Schemat blokowy rozpatrywanego obwodu, spełniający powyższe równania, podany jest na rys. 187

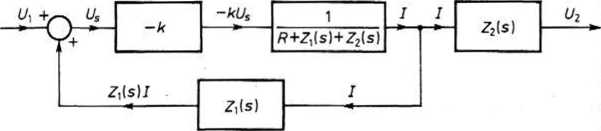
Rys. 18.7. Schemat blokowy obwodu z rys. 18.6

18.2.2. Połączenie łańcuchowe i połączenie równoległe

Połączenie łańcuchowe członów otrzymuje się, gdy sygnał wyjściowy jednego członu doprowadza się do wejścia następnego członu (rys. 18.8), przy czym X(s) jest sygnałem wejściowym, a Y(.sj — sygnałem wyjściowym połączenia.

Rys. 18.8. Połączenie łańcuchowe trzech członów

Na podstawie określenia transmitancji otrzymujemy dla każdego członu zawartego w połączeniu następujące równania:

Yi(s) = WX(s), y₂(s) = T₂(s) Y_t(s), Y(s) = T₃(s)Y₂(s).

Po wymnożeniu stronami tych równań, znajdujemy

Y{s) = T_l(s)T₂(s)T₃(s)X(s),

wobec tego transmitancja połączenia wynosi

Y(s)

^r(s)=^^=r*^(s)r>^(s)r>^(s)- ^(18J)

Transmitancja połączenia łańcuchowego równa się iloczynowi transmitancji członów wchodzących w skład połączenia. Powyższy wynik jest ogólny i dotyczy połączenia łańcuchowego dowolnej liczby członów.

Rozważania te są słuszne przy założeniu, że człon dołączony do wejścia poprzedniego członu nie obciąża tego członu, czyli gdy dołączenie członu nie zmienia sygnału wyjściowego członu poprzedniego.

Połączenie równoległe dwóch członów przedstawione jest na rys. 18.9, przy czym _w węźle sumacyjnym sygnały dodają się lub odejmują. Na podstawie rys. 18.9

znajdujemy

y, (s) = T, (s)X(s),    y₂(s) = T₂(s)X(s),

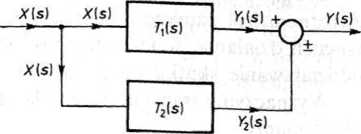
Rys. 18.9. Połączenie równoległe dwóch członów

zgodnie z określeniem transmitancji, a ponadto

y(s) = y,(s)± y₂(s),

wobec tego

Y(s) = ms)±T₂(s)-]X(s). Transmitancja połączenia równoległego wynosi zatem

(18.2)

T(s) = ^=T₁(s)±T₂(s). X(s)

Transmitancja połączenia równoległego dwóch członów równa się sumie lub różnicy transmitancji członów wchodzących w skład połączenia, w zależności od tego, czy w węźle sumacyjnym sygnały dodają się, czy też odejmują.

18,3. Sprzężenie zwrotne

18.3.1. Zależności podstawowe

W układzie z rys. 18.10 sygnał wyjściowy y(s) członu 7j(s) kierujemy przez człon T₂(s) do wejścia układu, gdzie odejmuje się od sygnału wejściowego A^s) lub też dodaje się do tego sygnału. Rozpatrywany układ jest zamknięty, bowiem sygnał doprowadzony do wejścia członu 7j(s) obiega cały układ, przechodząc przez człony 7j(.s) oraz T,(s) i wraca po przekształceniu do wejścia członu Tj(.s). Z tego powodu sygnał wyjściowy członu T', (.s) wpływa na sygnał wejściowy AT, (.<?) tego członu.

X(s) X,(sl		r,(si	rls) ris)
y,is) Rys. 18.10. Schemat blokowy układu zc sprzężeniem				V(sl
	A	r2isi
zwrotnym