238 (22)

476

18. Schematy blokowe. Grafy sygnałowe Masona

(2) Przesunięcie węzła sumacyjnego zgodnie ze zwrotem sygnału. W pierwszym układzie z rys. 18.14 jest X₃ = T(s)(X, ±X₂), a w drugim układzie mamy X₃ = T(s)X_] ±T(s)X₂, wobec tego oba wyrażenia są jednakowe.

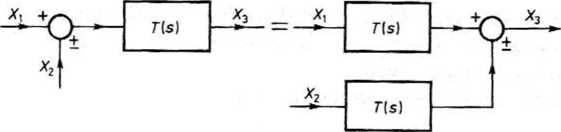
Rys 18.14. Przesunięcie węzła sumacyjnego zgodnie ze zwrotem sygnału

(3) Przesunięcie węzła sumacyjnego przeciwnie do zwrotu sygnału. W pierwszym układzie z rys. 18.15 spełnione jest równanie X₃ = T(s)X₁ ±X₂, a w drugim

układzie X₃ — T(s)

*i±

T(s)^Xz

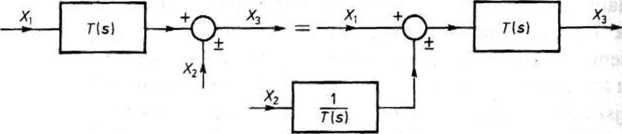
Rys. 18.15. Przesunięcie węzła sumacyjnego przeciwnie do zwrotu sygnału

, wobec tego oba wyrażenia są jednakowe.

(4) Przesunięcie węzła rozgałęźnego zgodnie ze zwrotem sygnału. Dla każdego układu na rys. 18.16 mamy X₂ = T(s)X_x, zaś sygnał odpływający od członu

o transmitancji 1/T(.s) jest równy X_t = T(s)X_l—, wobec tego dla sygnału X₂

T(s)

otrzymujemy takie same równania, a sygnał X_x jest nie zmieniony.

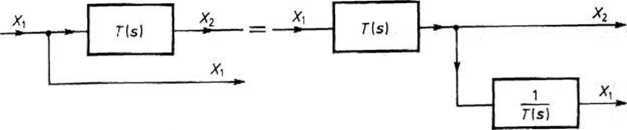
Rys. 18.16. Przesunięcie węzła rozgałęźnego zgodnie zc zwrotem sygnału

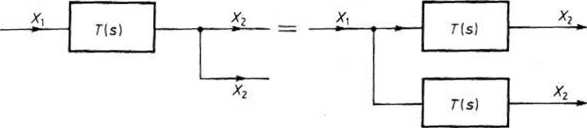
Rys. 18.17. Przesunięcie węzła rozgałęźnego przeciwnie do zwrotu sygnału

18.4. Przekształcanie schematów blokowych

477

(5)    Przesunięcie węzła rozgałęźnego przeciwnie do zwrotu sygnału. Sygnał X₂ w obu torach każdego układu z rys. 18.17 wynosi X₂ = T(s)X,, co dowodzi słuszności przekształcenia.

(6)    Zamiana układu ze sprzężeniem zwrotnym na pojedynczy człon. Przekształcenie układu z rys. 18.18 wynika wprost ze wzoru (18.3).

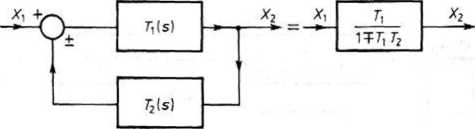
Rys. 18.18. Przekształcenie układu ze sprzężeniem zwrotnym

(7) Usunięcie członu z pętli sprzężenia zwrotnego. Transmitancja układu z rys. 18.19 nie zawierającego członu w pętli sprzężenia zwrotnego jest równa

_T() = J__T,(s)T₂(s) ₌    7j(s)

r₂(s)l TTJjJTjls) l + 7j(s)r₂(s)’

zgodnie z. wzorem (18.3), bowiem transmitancja pętli sprzężenia zwrotnego równa się 1. Taką samą transmitancję ma układ z rys. 18.19 z transmitancją T₂(s) w pętli sprzężenia zwTotnego.

Rys. 18.19. Usunięcie członu z pętli sprzężenia zwrotnego

(8) Zamiana członu na układ ze sprzężeniem zwrotnym. Transmitancja układu z rys. 18.20 ze sprzężeniem zwrotnym jest równa

T(s)

1 + T(s)

1

T(s)

1 + T(s)

= T(s),

Rys. 18.20. Zamiana członu na układ ze sprzężeniem zwrotnym