243 (20)

486 18. Schematy blokowe. Grafy sygnałowe Masona

węzłem, co pozwala obliczyć sygnał tego węzła w zależności od wymuszenia. Obliczenia wykonuje się dwiema metodami:

—    metodą kolejnych uproszczeń grafu sygnałowego przez eliminację poszczególnych węzłów i gałęzi albo

—    metodą analityczną.

Obie te metody zostaną omówione w toku dalszych rozważań.

18.7. Przekształcanie grafów sygnałowych Masona

Rozpatrzymy kilka podstawowych reguł umożliwiających uproszczenie grafów

sygnałowych Masona.

(1)    Połączenie łańcuchowe. Transmitancja połączenia łańcuchowego gałęzi równa się iloczynowi transmitancji tych gałęzi.

X,_a    X₂_b_X₃ _ X,_ab_X₃

Rys. 18.39. Przekształcenie połączenia łańcuchowego dwóch gałęzi

Istotnie, na podstawie rys. 18.39 otrzymujemy X₂ = aX_x oraz X₃ = bX₂, wobec tego X₃ = abX_t. Równanie to dotyczy uproszczonego połączenia z rys. 18.39. Po wykonaniu przekształcenia z rys. 18.39 eliminujemy węzeł X₂, co odpowiada eliminacji zmiennej X₂ z układu równań.

(2)    Połączenie równolegle. Transmitancja równoległego połączenia dwóch gałęzi równa się sumie transmitancji tych gałęzi.

Istotnie, zgodnie z rys. 18.40 mamy X₂ = aX_x+bX₃ = (a+b)X_l, co tłumaczy omawiane przekształcenie.

a

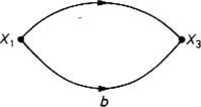
Rys. 18.40. Przekształcenie połączenia równoległego dwóch gałęzi

(3)    Eliminacja węzła nie zawierającego pętli własnej.

W przypadku rys. 18.41 otrzymuje się X₂ = bX₄ oraz X₃ = cX_Ą, przy czym X₄ = aXi, a po podstawieniu tej równości mamy X₂ = abX_x oraz X₃ = acX_x, co uzasadnia omawiane przekształcenie.

(4)    Eliminacja gałęzi grafu.

W przypadku grafu z rys. 18.42 mamy X_s = aX_x + cX₃ oraz X₂ = bX₅, wobec tego X₂ = b{aX_l d-cA',) = abX, + bcX₃, co uzasadnia przekształcenie.

151 Eliminacia netli.

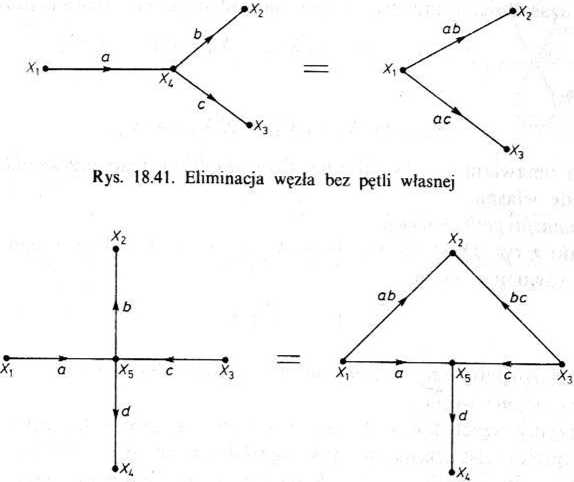
Rys. 18.42. Eliminacja gałęzi o transmitancji b

Rys. 18.43. Eliminacja pętli

*

*2 c X₃    X,    X₂    X₃

Rys. 18.44. Eliminacja pętli własnej

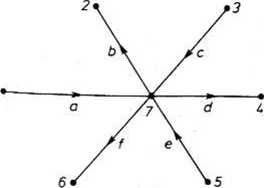
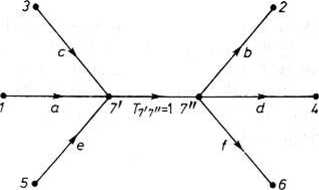
Rys. 18.45. Rozszerzenie węzła