241 (20)

482

t8. Schematy blokowe. Grafy sygnałowe Masona

2

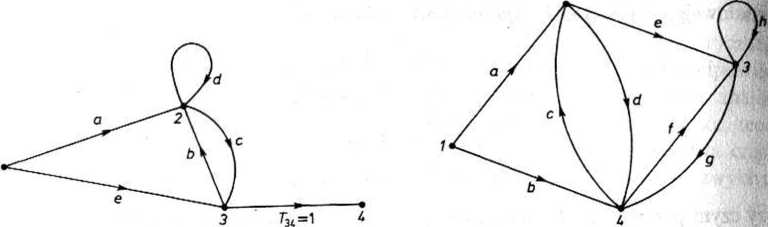
Rys. 18.28. Graf sygnałowy Masona zawierający Rys. 18.29. Graf sygnałowy Masona o 4 węzłach pętlę własną

Ścieżką otwartą nazywamy ścieżkę, która nie przechodzi dwukrotnie przez żaden węzeł. Przykładem ścieżki otwartej na rys. 18.29 jest ścieżka aeg lub adf.

Pętlą nazywamy ścieżkę zamkniętą, która zaczyna się w jednym węźle, kończy się w tym samym węźle i nie przechodzi dwukrotnie przez żaden węzeł pośredni. Przykładem pętli na rys. 18.29 są ścieżki cd, fg, egc oraz w przypadku szczególnym pętla własna h. Transmitancją pętli nazywamy iloczyn transmitancji wszystkich gałęzi tworzących pętlę.

18.6. Wyznaczanie grafów sygnałowych Masona

Z przykładów podanych w p. 18.5 wynika, że dla sygnałów poszczególnych węzłów otrzymuje się zależności liniowe. Z tego powodu za pomocą grafów sygnałowych można odwzorować równania 'iniowych obwodów elektrycznych.

W celu wyjaśnienia metody wyznaczania grafów sygnałowych, rozpatrzymy układ równań liniowych

^a21^l +^a22-^2 + ^a23^3 ⁼ 0> ^a31-^l“h^a32-^^r2“ł“^a33^3 ⁼ 0 .

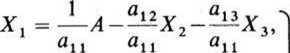
Z tych równań wyznaczamy kolejno wielkości X_t, X₂, X₂:

>

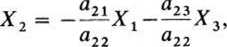
(18.15)

483

r

18.6. Wyznaczanie grafów sygnałowych Masona

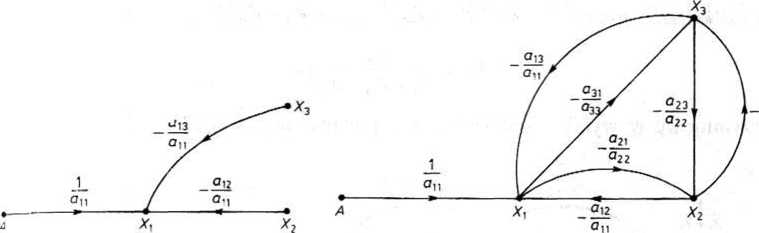
następnie rysujemy 4 węzły odpowiadające sygnałom X_lt X₂, X₃ oraz A. Rozpa-• rując kolejne wyrazy otrzymanych równań, rysujemy odpowiednie gałęzie grafu jV'jnałowego wraz z transmitancjami. Wynik odwzorowania pierwszego równania _ukladu (18.15) przedstawiony jest na rys. 18.30. Otrzymany wynik łatwo sprawdzić,

°32

°33

Rys. 18.31. Realizacja układu równań (18.15)

Rys. 18.30. Realizacja równania

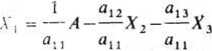
układając równanie dla węzła X_x przy zastosowaniu zasad omówionych w p. 18.5. Po odwzorowaniu wszystkich równań otrzymuje się graf sygnałowy Masona z rys.

18.31.

Przy wyznaczaniu grafów' sygnałowych Masona dla obwodów elektrycznych można wykorzystać równania napisane na podstawie praw KirchhołTa, bądź też równania Oczkowe lub węzłowe. W przypadku stosowania równań Oczkowych lub węzłowych sygnałami są odpowiednio prądy oczkowe lub napięcia węzłowe.

18.32. Przykład obwodu elektrycznego

"i

»

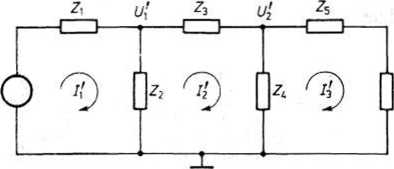
Rozpatrzymy obwód z rys. 18.32. Układając równania oczkowe, otrzymujemy

(Z,+Z₂)/j-Z₂/'₂ = U,

—z,/j +(z₂+z₃+zj/'₂-z₄r₃ = o,

-Z₄/₂ + (Z₄ + Z₅ + Z₆)/₃ = o.