239 (20)

478 18. Schematy blokowe. Grafy sygnałowe Masona

bowiem transmitancja pętli sprzężenia zwrotnego równa się 1. Otrzymany wynik dowodzi słuszności omawianego przekształcenia.

Zastosowanie omawianych reguł do przekształcania schematów blokowych przy wyznaczaniu transmitancji układu ilustrują przykłady.

Przykład 1. Przekształcimy schemat blokowy i rys. 18.7 i wyznaczymy transmitancję T(s) = i/₂(s)/C/ ,(.%•).

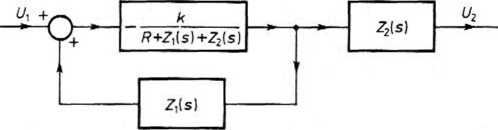
Rys. 18.21. Przekształcony schemat blokowy z rys. 18.7

Zastępując połączenie łańcuchowe dwóch transmitancji na rys. 18.7 jednym członem, otrzymujemy układ z rys. 18.21. Transmitancja układu ze sprzężeniem zwrotnym zawierającego transmitancję Z,(s) w pętli sprzężenia zwrotnego wynosi

R + Z_t (s) + Z₂ (s)

-k

R + ZAs)+Z-, (s)

z AA

-k

R+{k + 1 )Z ^(s) Z₂(s)

1 —

Rys. 18.22. Przekształcony schemat blokowy z rys. 18.21

wobec tego otrzymujemy układ z rys. 18.22 będący połączeniem łańcuchowym dwóch członów. Transmitancja układu z rys. 18.7 jest zatem równa iloczynowi transmitancji członów z rys. 18.22, w związku z tym

b'₂(s)    — kZ₂(x)

T(s) =-=---.

Lf,(s) R+(k+l)Z,(s)+Z,(s)

Transmitancję tę można oczywiście otrzymać wprost z rys. 18.6.

Przykład 2. Przekształcimy schemat blokowy z rys. 18.5 i obliczymy transmitancję T(s) = U₃(s)/L/,(s)-Przesuwając zgodnie ze zwrotem sygnału węzeł rozgałężny w schemacie blokowym z rys. 18.5, otrzymujemy przy zastosowaniu reguły 4 układ z rys. 18.23. Następnie przy zastosowaniu reguły

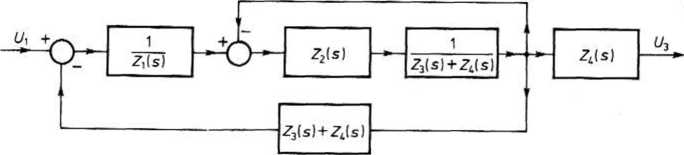
Rys. 18.23. Przekształcony schemat blokowy z rys. 18.5

6 przekształcimy układ ze sprzężeniem zwrotnym zawierającym połączenie łańcuchowe członów w torze głównym i nie zawierającym członu w pętli sprzężenia zwrotnego. Transmitancja tego układu wynosi

Z₂(s)

Z₃(s)+Z₄(s)    Z₂(s)

_{    Z₂(s)    Z₂(s) + Z₃(s)+Z₄(s)’

⁺ Z₃(s) + Z₄(s)

wobec tego otrzymuje się układ podany na rys. 18.24.

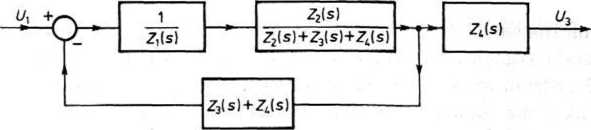
Rys. 18.24. Przekształcony schemat blokowy z rys. 18.23

Otrzymany schemat blokowy zawiera układ ze sprzężeniem zwrotnym, a w jego torze głównym znajduje się połączenie łańcuchowe dwóch członów. Transmitancja tego układu ze sprzężeniem zwrotnym

równa się

_Z,(Z₂ + Z₃ + Z₄)___ Z₂_

.__Z2_. +Z )    ^Z>(^Z2 ^{+ Z}3+^Z4) + Z₂(Z₃ + Z₄)

z,(z₂+z₃+z₄r³    4

u,	Z2			ió
	Z,(Z2+73+Z4)+Z2(Z3+Zt)

Rys. 18.25. Przekształcony schemat blokowy z rys. 18.24

a przekształcony układ przybiera postać połączenia łańcuchowego dwóch członów, jak na rys. 18.25. Wobec tego transmitancja rozpatrywanego układu wyraża się wzorem

U As)    Z₂Z₄

T(s) - W’. = -i—t-.

UAs) Z,(Z₂ + Z₃ + Z₄) + Z₂(Z₃ + Z₄)

Łatwo sprawdzić, że tę transmitancję można również otrzymać wprost z rys. 18.4.

18.5. Grafy sygnałowe Masona

Grafem sygnałowym Masona nazywamy zbiór węzłów oraz gałęzi łączących te węzły. Każda gałąź grafu sygnałowego ma zwrot określający przepływ sygnału od jednego węzła do drugiego, a przy przepływie wzdłuż gałęzi sygnał ulega przekształceniu. Grafy sygnałowe stanowią graficzne odwzorowanie układu równań opisującego badany układ fizyczny, podobnie jak schematy blokowe.

Grafy sygnałowe Masona obwodów elektrycznych mają zupełnie inną postać niż