237 (19)

474 18. Schematy blokowe. Grafy sygnałowe Masona

dwóch przypadków: 1) przy t₂ > 0, tzn. gdy kfj < 1 oraz 2) przy Tj < 0, tzn. gdy kp>\.

Postać przebiegu odpowiedzi impulsowej zależy od parametrów k, j? rozpatrywanego układu. Przy kfi > 1 odpowiedź impulsowa omawianego układu wzrasta

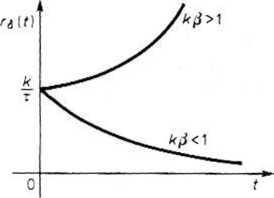
Rys. 18.12. Przebiegi odpowiedzi impulsowej układu ze sprzężeniem zwrotnym

wykładniczo do nieskończoności, w^robec tego układ ten jest niestabilny. Stwierdzamy zatem, że dodanie pętli sprzężenia zwrotnego może spowodować, że układ stanie się niestabilnym.

18.3.2. Sprzężenia zwrotne dodatnie i ujemne

Transmitancję widmową układu ze sprzężeniem zwrotnym otrzymujemy, podstawiając s=ju) do wzoru (18.3); mamy

T(jot) =

TjM

1 ± 7j(jft))T₂(ju>)‘

(18.9)

Sprzężenie zwrotne nazywamy dodatnim (regeneracyjnym), gdy 11 ± Tj (ja>) T₂ (jo))| < 1, a ujemnym (degeneracyjnym), gdy |1 ± Tj(jco)T₂(ja>)| > 1. Sprzężenie zwrotne może być ujemne w jednych zakresach pulsacji, a dodatnie w innych. W przypadku dodatniego sprzężenia zwrotnego mamy

|7'(jcó)| > |7j(ja>)|,

a w przypadku ujemnego sprzężenia zwrotnego

IT (j o>)| < |7j(jo))|.

Różniczkując wyrażenie T(ja)) ze wzoru (18.9) względem 7j(ja>), otrzymujemy

dT(jo))    1

t żyli

d7j(j<w) [1 ± 7j(jo))T₂(jo))]² ’

_ł2dTj(jo)),

dr(jo)) =

1

[1 ± T\(jco)X₂(j^)]²

(18.10)

a stąd. dzieląc stronami powyższy wzór przez zależność (18.9), znajdujemy

dr(jcu) ₌    1_d7j(jaj)

T()co) ~ \±T₁(jco)T₂{j(o) TM) '

Moduł tego wyrażenia przedstawia względną zmianę transmitancji widmowej T(ja>) układu ze sprzężeniem zwrotnym w zależności od względnej zmiany transmitancji widmowej "^(jco) toru głównego.

Dla ujemnego sprzężenia zwrotnego mamy

d7(jco)		d7j(jcu)
7(j<«)		TM)

(18.12)

dla dodatniego zaś sprzężenia zwrotnego

dT(jco)		d TM)
T(joi)		TM)

(18.13)

Przy zmianie parametrów toru głównego zmienia się również jego transmitancja widmowa 7j(jo>), co powoduje zmianę transmitancji widmowej T(jo>) układu ze sprzężeniem zwrotnym. Na podstawie nierówności (18.12) i (18.13) stwierdzamy, że względna zmiana transmitancji widmowej układu z ujemnym sprzężeniem zwrotnym jest mniejsza od względnej zmiany transmitancji widmowej toru głównego. Jeśli na przykład |1 + T,(jcu)T₂(joj)| = 10, to zmiana modułu transmitancji widmowej toru głównego o 5% powoduje zmianę transmitancji widmowej całego układu o 0,5%. Oznacza to, że ujemne sprzężenie zwrotne działa stabilizująco na transmitancję układu ze sprzężeniem zwrotnym.

Działanie dodatniego sprzężenia zwrotnego jest przeciwne, tzn. zmiana modułu transmitancji widmowej całego układu jest większa niż zmiana transmitancji toru

główmego.

18.4. Przekształcanie schematów blokowych

Dozwolone są następujące przekształcenia schematów blokowych (na rysunkach ilustrujących te reguły oraz przy uzasadnianiu przekształceń pominiemy dla uproszczenia zmienną s):

(1) Zamiana kolejności dodawania w węzłach sumacyjnych. Dla układu pierwszego (licząc od lewej strony) na rys. 18.13 mamy (X_x ±X₂)±X₃ = X₄, a dla układu drugiego (X, ±2Ć₃)± X₂ = X_A, co dowodzi słuszności omawianego przekształcenia.

Xy +S

	±	±
x2	X3	*3

IR H. Zamiana kolejności dodawania w węzłach sumacyjnych

Or

Puc