23 luty 07 (135)

Grafoanalityczna metoda wyznaczania reakcji dynamicznych w parach kinematycznych wybranych mechanizmów płaskich zawierających wyłącznie grupy ki. 2 przedstawiona zostanie na przykładach. We wszystkich przedstawionych poniżej przykładach człon 1 jest członem napędzającym i tarcie nie występuje. Sposób wyznaczania reakcji z uwzględnieniem tarcia przedstawiony zostanie w następnym podrozdziale.

Przykład 3.2

Mechanizm korbowo-suwakowy

Przeprowadzić analizę kinetostatyczną mechanizmu korbowo-suwakowego metodą grafoanalityczną w położeniu zadanym na rysunku 3.17. Wyznaczyć reakcje dynamiczne w parach kinematycznych oraz moment równoważący M_r1 przyłożony do korby 1. Tarcie w parach kinematycznych należy pominąć.

Dany jest: opis ruchu członu napędzającego w postaci funkcji: (p_1t (o_1t e_1t długości członów: AB, BC, AS_1t BS₂, masy członów m₁,m₂,m₃, momenty bezwładności członów względem środków mas: J_Sł,J_S2 oraz siła oporu P₃. Mechanizm pracuje w płaszczyźnie pionowej.

1 B 2

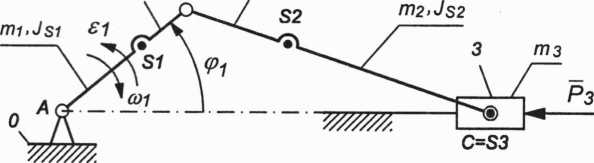
Rys. 3.17. Mechanizm korbowo-suwakowy

Rozwiązanie

Mechanizm składa się z członu napędzającego 1 oraz grupy strukturalnej (2, 3) klasy 2. Ruchliwość mechanizmu jest równa w = 1.

Warunek statycznej wyznaczalności mechanizmu określony równaniem (3.19) jest spełniony, ponieważ: 3-3 = 2-4 +1 = 9.

Przyśpieszenia liniowe środków mas: a_s1, a_S2, a₃₃ oraz przyśpieszenia kątowe członów e₂ i e₃ zostały wyznaczone na podstawie planu przyspieszeń przedstawionego na rysunku 3.3. Obliczamy siły bezwładności oraz momenty od sił bezwładności członów na podstawie wzorów (3.11) do (3.16) i przykładamy je do mechanizmu zgodnie z rysunkami 3.4, 3.5 oraz 3.6:

człon 1: B-, = -m-,a_s1,    B₁    = m_ya_Sł,    M_B1 = -J_SJe_r,    M_B1 = J_Sfe_t;

człon 2: B₂ = —m₂a_B2,    B₂    — m₂a_B2,    M_B2 = ~Js2^2<    M_B2 ~ ^S2^2’

człon 3: B₃ = -m₃a_S3,    B₃    = m₃a_S3,    M_B3 = -J_S30 = 0,    M_B3 = 0.

134