244 [1024x768]

ELEMENTY TERMODYNAMIKI STATYSTYCZNEJ

ELEMENTY TERMODYNAMIKI STATYSTYCZNEJ

(3.182)

oraz z równań (3.170) i (3.181): F = -*rin<2

W praktycznych zastosowaniach ważniejsza jest znajomość entalpii swobodnej (3.44)

G = F+pY

Należy w tym celu znaleźć wyrażenie na ciśnienie; ponieważ (3.64)

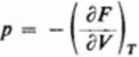
zatem z (3.182) otrzymamy:

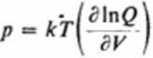
(3.183)

a stąd i z równania (3.44):

c--*r_ta(?₊*r(^e)_r

(3.184)

Przykłady wyrażeń na sumę stanów

Całkowita energia wewnętrzna cząsteczki jest sumą energii translacyjnej, elektronowej, oscylacyjnej, rotacyjnej i innych.

Załóżmy dla uproszczenia, że ruchy cząsteczki odbywają się w sposób niezależny; umożliwi nam to wyrażenie całkowitej sumy stanów jako iloczynu sum stanów poszczególnych rodzajów energii:

(3.185)

Całkowita

energia

WEWNĘTRZNA

CZĄSTECZKI

0-O*

Równanie to wynika stąd, że jeżeli

U i - U_u„. + U_tl + U_ote + U_rot

to po wstawieniu tej wartości do wyrażenia na sumę stanów (3.172) /

e-5V«-^włT

/.i

otrzymuje się równanie (3.185).