240 [1024x768]

ELEMENTY TERMODYNAMIKI STATYSTYCZNEJ

Różniczkując to równanie obustronnie względem T (w stałej objętości)

_kT> i*"--'-*⁷

!• I

oraz dzieląc obustronnie pr/cz </, otrzymujemy:

/

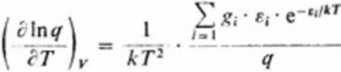
(3.168)

Stąd z równania (3.167) otrzymujemy wyrażenie na średnią energię jednej cząsteczki w postaci:

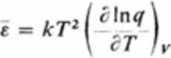
(3.169)

które przechodzi w równanie na energię wewnętrzną 1 mola cząsteczek po pomnożeniu przez liczbę Avogadra:

U = N₄e =    (3170)

W równaniu tym Q oznacza tzw. wielką sumę stanów

Q - <r^s    (3.171)

zwaną także molową funkcją podzia/u; przy wykorzystaniu (3.163) możemy także napisać:

(3.172)

Wielka

suma

STANÓW

Związek pomiędzy sumą stanów ą a wielką sumą stanów Q, określony równaniem (3.171), spełniony jest'jedynie w takich układach, w których cząsteczki ze względu na dany rodzaj energii są odróżnialne. Jeżeli ze względu na pewien rodzaj energii (np. energii ruchu translacyjncgo w gazie) cząsteczki są nieodróżnialne, to w miejsce równania (3.171) spełnione jest wyrażenie:

<2 =

<r^s

N\

(3.173)

Pochodzenie członu jV! w mianowniku, podającego liczbę wszystkich możliwych uporządkowań zbioru N cząsteczek, stanie się zrozumiałe po rozważeniu prawdopodobieństwa termodynamicznego (str. 248).