251 (44)

.0.4/251
ODY ROZWIĄZYWANIA WirLKJCII UKŁADÓW LINIOWYCH...
osując eliminację Gaussa dochodzimy do następujących wzorów (szczególny —rpadck wzorów' z p. 6.6.2):
(10.116)
I y, = «!+! yi+i+Ai+i i = n-i, x-2,i
\>iV = fis I-1
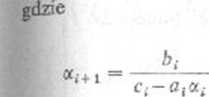
i = 2, ..., xV—1, . «2 = btlci
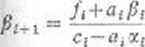
= 2, ...» A/ > =/1/c1
.2 Tak więc algorytm ten składa się z dwfóch etapów. W pierwszym obliczamy współ
czynniki i w drugim zaś — rozwiązania y\. Należy wyjaśnić przy jakich założeniach o współczynnikach rozpatrywany układ jest nieosobliwy i kiedy algorytm ten jest numerycznie poprawmy. Warunki dostateczne są zawarte w następującym lemacie.
Lemat 10.10
Jeśli współczynniki Cj, cv, ó.-, i = 2. .... N— ł są różne od zera oraz
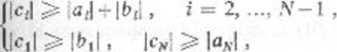
(10.117)
przy czym co najmniej w jednej z nierówności w (10.117) zachodzi ostra nierówność, to układ (10.115) ma jednoznaczne rozwiązanie i algorytm (10.116) jest
numerycznie poprawny.
Dowód tezy pierwszej można znaleźć np. w książce [95], drugiej zaś — v-’ artykule [48].
Analizując algorytm (10.116) widzimy, że koszt jego wynosi rzędu A działań arytmetycznych i wymaga tyle samo miejsc pamięci. Co do rzędu liczby działań * obciążenia pamięci algorytm ten jest optymalny (por. p. 1.?). Przedstawiony algorytm jest szczególnym przypadkiem algorytmu dla macierzy wstęgowej opisanego w artykule w [126]. Tam też podane są procedury rozwiązywania takich układów.
orytm korzystający z FFT 10.4.3
amy teraz szybki algorytm rozwiązywania zadań różnicowych aproksymują-t równanie Poissona w prostokącie z warunkami Dirichlcta (dla ustalenia gi będziemy zakładać, że są one jednorodne). Algorytm ter. jest połączeniem rytmów' rozwiązywania układów z macierzą irójdiagonaimi (zob. p. 10.4.2) bkich przekształceń Fouriera (FFT). (zob. p. 2.6.2).

Wyszukiwarka
Podobne podstrony:
257 (44) ODY ROZWIĄZYWANIA WIELKICH UKŁADÓW LINIOWYCH...iS/257 Zauważmy, że zadania (10.123) i (10.1
259 (39) ODY ROZWIĄZYWANIA WIELKICH UKŁADÓW LINIOWYCH... ,4/259 la przestrzeń elementu skończonego F
263 (41) ODY ROZWIĄZYWANIA WIELKICH UKŁADÓW LINIOWYCH...id ą/263 są mniejsze co do modułu od jednośc
sc0009 bmp Rozwiązywanie układu równań liniowych metodą eliminacji Gaussa Metoda eliminacji K. Gauss
253 (44) r DY ROZWIĄZYWANIA WIELKICH UKŁADÓW LINIOWYCH... io.4/253 Przekształćmy układ (10.119)
261 (41) j/fc-TODY ROZWIĄZYWANIA WIELKICH UKŁADÓW LINIOWYCH...
267 (40) METODY ROZWIĄZYWANIA WIELKICH UKŁADÓW LINIOWYCH... 10.4/267 Dowód łicrówność lewostronna wy
269 (42) ; METODY ROZWIĄZYWANIA WIELKICH UKŁADÓW LINIOWYCH... 10.4/269 krok iteracji .sprowadza się
44 Badanie kliniczne w neurologii poziomą (sitową) kości sitowej, wypustki dośrodkowe dochodzą do op
4 Wykład 1. Metody numeryczne - równania liniowe 1.0.2. Algorytm eliminacji Gaussa-Jordana Najbardzi
s130 131 130 5. Rozwiązać układy równań liniowych: (a) x — y 4- 2z — 4 2x + y — 3z = 6 ( x - 2y + z
skanowanie7 (3) 2.30. Podane funkcje są rozwiązaniami wskazanych równań liniowych niciednorodnvch. W
więcej podobnych podstron