269 (2)

38 Co to jest wartość dlo akcjonariuszy?
w porównaniach obligacjami o odpowiednim terminie zapadalności. Dochody te lepiej służą celom porównawczym niż wszelkie stopy procentowe oferowane aktualnie za lokaty krótkoterminowe, ponieważ lokaty takie będą przenoszone na następne terminy, a trudno przewidzieć, czy stopy oprocentowania w kolejnych terminach będą stałe przez cały okres przedsięwzięcia. Zazwyczaj tak się nie dzieje, dlatego preferujemy stopy obligacji długoterminowych.
Tak się jednak składa, że mówiąc o dostępnych na rynku stopach procentowych, możemy niekiedy mieć trudności z określeniem, o który właściwie rynek chodzi. Naszym zdaniem, analiza SHV powinna dążyć do zachowania jak najbardziej lokalnego charakteru wszystkich danych, przynajmniej na wstępie. Ważne jest, gdzie spółka wypłaca dywidendy - a wypłaca je we własnym kraju. Zwrot z inwestycji będzie więc realizowany w krajowej walucie i w jakiś sposób musi odzwierciedlać aktualne stopy procentowe dostępne na rynku.
Sytuacja może się znacznie bardziej skomplikować, kiedy duża korporacja zaciągnęła sporo pożyczek w wielu różnych walutach lub jest zarejestrowana w kilku państwach. Bardziej szczegółowe omówienie takiej sytuacji przedstawimy w dalszej części książki.
Współczynniki beta (p)
Dlaczego ważne są współczynniki beta? Dlaczego ekonomiści poświęcają im aż tak wiele uwagi? Współczynnik beta jest miarą związku zachodzącego między zmianami w cenie danej akcji a zmianami w odnośnym indeksie rynku akcji (share index). Umożliwia dokonanie pomiaru systematycznego ryzyka podejmowanego przez inwestora kupującego tę akcję i daje pojęcie o tym, na ile ruchy cenowe tej akcji będą zbieżne z rynkiem. Jest to ważne, ponieważ choć inwestorzy mogą równoważyć konkretne ryzyko związane z poszczególnymi akcjami poprzez prowadzenie zróżnicowanego portfela, to jednak są nadal wystawieni na systematyczne ryzyko związane z całością rynku, którego już nie uda się zrównoważyć dywersyfikacją. Im wyższy współczynnik beta danej akcji, tym większe związane z nią ryzyko. Tak więc akcja o współczynniku większym od jeden wykonuje większe ruchy cenowe niż rynek, dlatego nazywa się ją niekiedy akcją zmiennej ceny (volatile share). Cena akcji o współczynniku beta mniejszym od jeden wykonuje ruchy mniejsze niż cały rynek, a akcję tę określa się mianem inwestycji defensywnej (zob. ilustr. 3.1).
Pociąga to za sobą wiele implikacji dotyczących stóp zwrotu, jakich wymaga się od danej akcji. Opracowanie Frienda i Blume’a1 wskazuje na powiązanie współczynników beta akcji (tu: zebranych w portfele) z późniejszymi wynikami akcji. Opracowanie to podaje wyniki przedstawione w tabeli 3.1, której dolną część zajmują portfele najbardziej ryzykowne.
Bieżąca
13%
11%
8%
= 7%
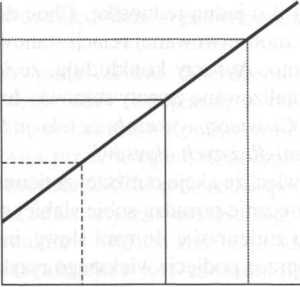
W miarę wzrostu współczynnika 8 wzrasta minimalna wymagana stopa zwrotu
0,5 1,0
1,5 Beta
stopa
zwrotu
Ilustracja 3.1. Wymagana przez inwestorów stopa zwrotu
W tabeli 3.1 przedstawiono średnie stopy zwrotu szeregu portfeli inwestycyjnych wzrastające w miarę zwiększania się ryzyka. Co ciekawe, w pewnym punkcie średnia stopa zwrotu nie podnosi się jednak proporcjonalnie do wzrostu ryzyka, tak więc nie można wiele zyskać na tworzeniu portfeli bardzo ryzykownych. Innym interesującym zjawiskiem jest fakt, że rozdźwięk pomiędzy wynikami portfeli najbardziej ryzykownych i tych obciążonych najmniejszym ryzykiem wydaje się maleć z upływem czasu, potwierdzając opinię, że wzrasta efektywność rynków kapitałowych.
W innym opracowaniu jego autorzy, Black, Jensen i Scholes2, prezentując charakterystykę różnych amerykańskich akcji w odniesieniu do relacji ryzyka do stopy zwrotu na przestrzeni 35 lat, dochodzą do wniosku, że średnia rentowność tych akcji wzrastała o 1,08% miesięcznie (13% w skali roku) na każ-
Tabela 3.1. Większe ryzyko to większy zwrot, ale mniejszy niż przewidywania na podstawie modelu CAPM
|
Portfel |
1939-1969 |
1948-1969 |
1956-1969 | |||
|
P |
średnia stopa zwrotu (%) |
P |
średnia stopa zwrotu (%) |
P |
średnia stopa zwrotu (%) | |
|
1 |
0,19 |
0,79 |
0,45 |
0,99 |
0,28 |
0,95 |
|
2 |
0,92 |
1,26 |
0,94 |
1,35 |
0,91 |
1,17 |
|
3 |
1,29 |
1,53 |
1,23 |
1,33 |
1,3 |
1,18 |
|
4 |
2,02 |
1,59 |
1,67 |
1,36 |
1,92 |
1,10 |
Źródło: Friend i Blume,/1 New Look.op. cit.
A New Look at the Capital Asset Pricing Model, „Journal of Finance”, 1973, s. 19-33.
F. Black, M. Jensen i M. Scholes, The Capital Asset Pricing Model: some empirical tests, [w:] Studies in the Theory of Capital Markets, Praeger, 1972.
Wyszukiwarka
Podobne podstrony:
271 (2) 42 Co to jest wartość dla akcjonariuszy? średnią arytmetyczną nadwyżkowych zwrotów z kapitai
44 Co to jest wartość dla akcjonariuszy? przy niewątpliwym prymacie Wielkiej Brytanii pod tym względ
273 (2) 46 Co to jest wartość dla akcjonariuszy? najmniej pokryć koszt tego kapitału. Sposób, w jaki
48 Co to jest wartość dla akcjonariuszy? o współczynnik beta ceny akcji tej spółki - w tym wypadku 0
271 (2) 42 Co to jest wartość dla akcjonariuszy? średnią arytmetyczną nadwyżkowych zwrotów z kapitał
34 Co to jest wartość dla akcjonariuszy? Oto ogólne zagadnienia, które mają wpływ na konsultantów i
36 Co to jest wartość dla akcjonariuszy? szczęście. Roczny dochód dwadzieścia funtów, a roczne wydat
r J Co to jest wartość dla akcjonariuszy? dy wzrost współczynnika 6 o jedną jednostkę. Choć dowodził
skanuj0202 38 1. Co to jest strategia i zarządzanie strategiczne dań oraz oczekiwanych wyników; znac
scan0006 (38) 3.Co to jest auksolugia i jakie dziedziny / ocenę proporcji ciała pr
Kolokwium z tech?t 6 KOLOKWIUM Z TECHNOLOGU BETONU LABORATORIUM rok akad. 2005/06 38. Co to jest wsk
Durkheim socjologia07 38 /. Co to jest fakt społeczny? jąc się. To drugie kryterium jest nawet w pew
13. Co to jest wartość znormalizowana? Odpowiednia wartość/parametr podawana w odpowiedniej
więcej podobnych podstron