28 (663)

1. Układy płaskie w przypadku więzów idealnych

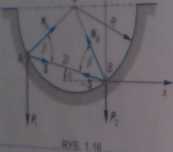
pągyKkAD 1.15 Dwie kulki A i B o ciężarach Pi i P₂ znajdują się w

równowagi wewnątrz gładkiej, sferycznej czaszy o pjw* R kulki są połączone nieważkim prętem o długości

Znaleźć naciski S_A i Nb kulek na czaszę, silę S%. AB oraz kąt a. jaki tworzy pręt AB z poziomem w poL równowagi (rys. 1.16).

Dwa jednorc w punkcie ( położono wi kątami er i /:

ROZWIĄZANIE

Przecinając myślowo pręt AB, rozdzielamy układ* układy proste. Siły działające na punkty A i B zaznacz* ryt 1.16. Korzystając z warunków równowagi dla punk; i B w postaci (1.1), dostajemy następujące cztery rówr_

' — S cos a 4- Na ćos(fi — a) = 0 -Pi 4- S sin a + Na sin(fi - a) = 0 Scoscr.— Nb cos(/3 4- a) = 0 -P₂ 4- Nb sin(fi 4- ot) — S sin a = 0 Z równań (l) i (2| (©trzymamy

5 sin fi * Pi cos (er — fi) a i równań (3) i (4)

S sin fi = P₂ cos(a 4- fi)

Na w alce A Z warunków

a i warunki

Wyliczamy

Z dra

2'ównart (l)+_{(4) ma}

sin/3

Stąd mamy związek

Pi cos(a fc» fi) = P₂ cos(a 4- fi)

Pb rozpisaniu otrzymamy

Pi cos a cos fi 4 Pi sin a sin fi = P₂ cos a cos ^-P; sina*

Po podzieleniu ostatnie] równości przez cos a cos p i waniu odpowiednich wyrażeń dostajemy

_tEa-fc-fi^)co^

<P₂4- Pi) sin

Na podstawie rys. 1.16 możemy napisać

- 1    -/P - P

«n fi-fT—j-. cos fi m

zatem

tger SB

(Pi - P\)l

(P2 + Pj)\/P² — l²

imy

Na

cos a

an f!

l

R

Pi, Pi r sinf

Zatem

Redl

Zredukował s/tywne do sil układem O, równowi rozumiemy

Z mech dukuje się nego M_g.

Współi