31 (614)

00

Punkty osobliwe i residua

mianownik nie ma pierwiastków rzeczywistych oraz jego stopień jest co najmniej o 2 większy od stopnia licznika.

O Ćwiczenie 5.4.4

Obliczyć podane całki niewłaściwe:

oo

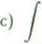
— oo

^d) / ⁴*² + 8* + 5^{:    b)} / (1 + x²)^{3 1}

-oo    -OO

_    oo

Twierdzenie* 5.4.5 (zastosowanie residuów do obliczania całek J e'^azg(x) dx)

Niech /(z) = e'^a2g(z), gdzie a > 0 oraz g(z) jest funkcją holomorficzną w

pólplaszczyźnie Im z ^ 0 poza skończoną liczbą punktów zj, z₂.....z„ takich,

że Imzi > 0, Imz2 > 0,...,lmz_n > 0, a ponadto g(z)—>0, gdy z—>00 i Im z ^ 0. Wtedy

7

/ f(x) dx = 2iri    res „ /(z).

*=1

Uwaga*. Dla a < 0 prawdziwy jest wzór

7

/ f(x)dx = -2jri]T res_ik/(z),

-«    *=1

przy czym założenia odnośnie funkcji g(z) dotyczą dolnej pólplaszczyzny.

O Ćwiczenie* 5.4.6

Obliczyć podane całki niewłaściwe:

.    / z cos z dz    f cos 2zdz

^ł) J x’-2x + 10^{; b}> J T+15

— OO

5.5 Odpowiedzi i wskazówki

5.1.4 a) {z e C: 1 < |z| < 2}, /(z) = ^7 + 737 i

b) {z e C: 0 < |z| < 00}, /(z) = e' + e' - 1.

n= 1 n+1 n

■> ^+D-r ■    ») D-.C^ <iE?'

n = 0

3    3 • 2^n_1 TzL^3z"

5.1.8 1<H <2./w-i + i-Lj-1-^ = 1

|z| < 1, /(z) rozwija się w szereg Taylora.

_W>2,_/W = . ₊ fl±(_iłĘ£li.

Odpowiedzi i wskazówki

69

5.1.9 a) -

2{z + 2)

, 8rr + 20n + 11 I (2ti + 3)!    z²" '

.11 z z ,    ,    C_1    Co , Cl    C„_|

^e) I-2 ⁺ l2"72Ó⁺ •'^C-^{, = 1}' (^T^⁺(^T+T)! ⁺ ^T⁺ - ⁺~^{+Cn = 0dlil}

n = 0, 1,2,... .

5.1.10 Dla F(t) =

1

a + cos t

, gdzie a > 1, mamy

/(*) =

F(t) =

1

y/a² — 1 1

\/a² — 1

1 + E(-l)" (« ~ n/^T)" («- + z")

n=l

°o    ^

1+2    a + \/a¹ - ij cos nt

(2n + 2)!

5.2.5 a) y , ^{( 1)n},^^łn; b) V* J ^ł)" ,z⁴"; c) f\-l)ⁿ*²—'. ^;Z-/(2n + l)l    ^;    ' (2n + 2)!    ’ Z—’

5.2.8    a) zo = 0, 1-krotny; b) zo = 0, 3-krotny; c) zo = 0, 3-krotny, z* = kir, gdzie

2

k = ±1,±2,..., 1-krotne; d) Zk = fcir, gdzie k € Z, 2-krotne; e) zk = ^ 4."2l), ^ gdzie k € Z, 1-krotne.

5.2.10 a) zo = 0, z definicji; b) zo = 0, pokazać, że nie istnieje lim /(z);

*—0

c) zk = fcjr, gdzie k G Z, pokazać, że nie istnieje lim f(z).

x—»kn

5.3.3 a) resi/(z) = i, res_i/(z) = i; b) res₀/(z) = 1, res,/(z) = -y, res _,/(z) =

~~2~’ ^c) ^res2/(ⁱ) = 5> res_j/(z)= y res -i-./(z) = - y res -i + ,/(z) = - i.

11 8

5.3.5 a) resi/(z) = -, rcs_i/(z) =--; b) resj/(z) =    resj/(*)=l;

f-n*⁺¹

c)    resk»/(a) = (—1    , gdzie k e Z, <i) res ^_/(z) = ■ .₂ ^ ■, gdzie k e Z\ {0} .

5.3.8    a) res₂/(z) =    ^b) res₀/(z) =    c) reso/(z) =

d) res,/(z) = —i-————=■; e) reso/(*) = 0.

’    ^W 2^2n_1 [(n - l)!]²    K '    ^v

5.3.9    a) reso/(z) = -y b) resi/(z) = 2; c) res_j/(z) = 2sin 1.

(—Z    3ir \    _

e ⁴ + e ⁴ + e ⁴ j; f) -jti.

5.4.4 a) 2*; b) c)

5.4.6 a) yj(cos 1 — 3sin 1); b) —.